Lectures Text
Understanding of Mathematics
Preface
Contemporary mathematics can be used as an effective tool to serve purposes of the Quran, Hadith and Islamic jurisprudence. Many a times mathematics is required for a gainful use of these three. It is generally perceived that students of the religious seminaries sometimes are devoid of the requisite knowledge of the essential religious aspects because of the lack of understanding of mathematics, as the subject is not taught there. This impression may though not be totally correct but is partially true. Either the subject is not taught at all or where it included in the curriculum, religious considerations are ignored. I was surprised to see books prescribed for ‘adadia’ by the Wafaq ul Madaras which included mathematical aspect only needed by the engineers or scientists and had completely ignored the basic subjects needed by the religious scholars. During one of my trip to teach astronomy at Dar al Aloom, Karachi, introduction of an electronic calculator to solve difficult mathematical questions was not only well received by teachers and students alike but it also paid rich dividend. I was happily surprised to learn that a simple tool can be so effective to bridge the learning gap and save precious time. A gap purposely designed by the British to normal schools and religious seminaries apart. There is a dire need to introduce modern teachings tool in the Madarsas. It is strange to see that an effort to equip the madrasas with computers is there but a simple tool like a calculator is totally missing. Surely this is a positive step, but there is a need to provide simple calculators as well.
During the discussions on these matters in the Dar al Aloom, a need to write a basic book of mathematics encompassing the religious aspects was realized. I was asked the time frame for doing it. On my assertion to complete it in one month, the management very graciously asked me to complete it in three months. I am grateful to them for choosing me. May Allah Almighty reward them. Amen. By the grace and blessings of Allah Almighty and help from a few friends, I have written this book. May Allah Almighty do not deprive me of this knowledge because of the treachery of my self (naf’s). I make no tall claims about my knowledge of the contemporary mathematics. When the learned hesitate, some body has to take the initiative to give them a lead.
A glean through the subjects included in this book vividly shows that the emphasis is on making it useful rather than voluminous. Well wishers are requested not only to pray for me but also provide their candid advice to make it more rewarding for the students. At my end, I have constituted a committee to approve changes, Insha Allah.
Syed Shabbir Ahmed Kakakhel
Advisor Technical Matters, International Institute for Islamic Mathematical Facilitations, Rawalpindi
Chapter 1- Numbers
Introduction
In the day to day life, need to add, subtract, multiply and divide arise frequently. These have their own specific principles and rules. To do the very basic arithmetical computations one has to learn mathematics. Some of the simple principles are as follows.
Type of Numbers
Natural Numbers
A number is a count or measurement of objects. Starting with 1 these can go up to infinity. The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12… ………….are natural numbers.
Whole Numbers
Whole numbers are like the natural numbers but these begin with a 0 e.g. 0, 1, 2, 3, 4, 5, 6, 7, 8 ………………….. There is no fractional or decimal part in it.
Real Numbers
In these along with the natural numbers, as many negative numbers are also included e.g. …….-6,-5, -4,-3,-2,-1, 0. 1, 2, 3, 4, 5, 6, …………

Negative Numbers
In day to day situations, it is often not enough to use only whole numbers. Consider this example:-
Zaid had deposited Rs. 45 with Umro. He needed Rs.100 and took them from Umro.
45-100= - 55. Now Zaid owes Rs.55 to Umro. Negative numbers are opposite of the positive numbers. If positive are for credit then negative are for debt. Earlier Zaid had a saving of Rs.45 but now he is under a debt of Rs.55.
Even Numbers
Those numbers that can be divided by 2 are called even numbers e.g.2, 4, 6, 8, 10……………
Odd Numbers
Those numbers that can not be divided by 2 are called odd numbers e.g. 1, 3, 5, 7, 9, 11……………..
Integer

A number with no fractional part.
Includes the counting numbers {1, 2, 3, ...}, zero {0}, and the negative of the counting numbers {-1, -2, -3, ...}
You can write them down like this: {..., -3, -2, -1, 0, 1, 2, 3, ...}
Examples of integers: -16, -3, 0, 1, 198
Addition
To bring two or more numbers (or things) together to make a new total.
Here 1 ball is added to 1 ball to make 2 balls.
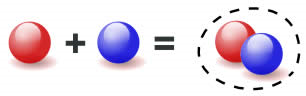
Or
2+3=5
It will be read as two plus three is equal to five.
+ is the symbol; for addition.
Subtraction
To take one number away from another.
If you have 5 apples and you subtract 2, you will be left with 3.
The symbol of subtraction is -
Example: 5 - 2 = 3

It is read as five minus two is equal to three.
Its symbol is ‘-‘.
Multiplication
The basic idea of multiplication is repeated addition.
For example: 5 × 3 = 5 + 5 + 5 = 15
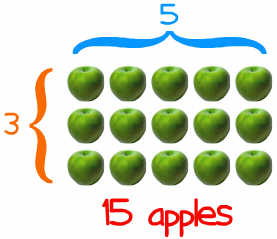
It is read as three multiplied by five is equal to fifteen.
Its symbol is ‘x’.
Division
Division is splitting into equal parts or groups. It is the result of "fair sharing".
Example: there are 12 chocolates, and 3 friends want to share them, how do they divide the chocolates?

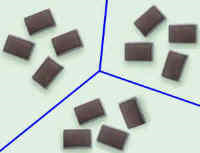
Answer: They should get 4 each.
We use the ÷ symbol, or sometimes the / symbol to mean divide:
12 / 3 = 4
12 ÷ 3 = 4
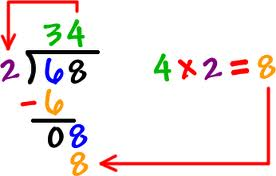
The other way of doing it as shown below :-
68 have been divided by 2. Answer is 32 and nothing is left. First of the division symbol is drawn, dividend is written inside and the divisor out on the left side. On top is the answer or the quotient. Then under the dividend is written the product of multiplication of divisor x quotient. After subtracting it from the dividend if nothing is left then division is complete, Some time we have a residual left after going through the above process which can not be divided any further.
Use of Electronic Calculator
It is being thankless not to use a calculator. It can save time which is a precious asset.
Decimal System
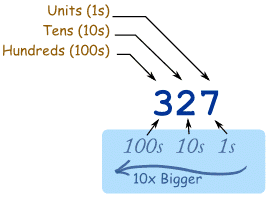
The number system we use every day, based on 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Position is important, with the first position being units, and then next on the left being tens, then hundreds and so on. Often "decimal number" is also used to mean a number that uses a decimal point followed by digits as a way of showing values less than one.
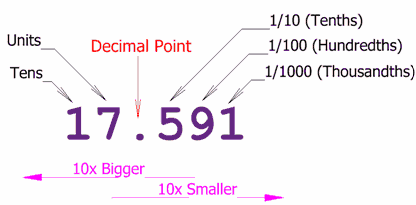
Example: 1.9 is a decimal number (one and nine tenths)
The decimal point is the most important part of a Decimal Number. It is exactly to the right of the Units position. Without it, we would be lost ... and not know what each position meant.
Now we can continue with smaller and smaller values, from tenths, to hundredths, and so on, like in this example:
Adding Decimals
To add decimals, follow these steps:
- Write down the numbers, one under the other, with the decimal points lined up
- Put in zeros so the numbers have the same length
- Then add normally, remembering to put the decimal point in the answer
Example: Add 1.452 to 1.3
Line the decimals up: 1.452 + 1.3 "Pad" with zeros: 1.452 + 1.300 Add: 1.452 + 1.300 ----- 2.752
Example: Add 3.25, 0.075 and 5
Line the decimals up: 3.25 0.075 + 5. "Pad" with zeros: 3.250 0.075 + 5.000 Add: 3.250 0.075 + 5.000 ----- 8.325
Exercise 1
Question 1
Abdul Qadir has to divide Rs.112 among five children. How much will a child get? How much more should be added to it to complete them for equal distribution?
Question 2Ali gave Rs.51to Saleem who bought him two books priced at Rs.22.75 and Rs.19.75. How much is left with him? Ali has liked the books and wants to buy those for his 11 students. How much more should he give to Saleem?
Question 3A youngster was killed in a road accident. Court has ordered the family of the driver to pay blood money (da’it) to the family of the deceased. Price of silver being Rs.102 per tola, work out the money to be paid? Da’it is 2625 tolas of silver.
Question 4During the nikkah ceremony of Rashida ‘Mehar e Fatimee’ was fixed as the dower. Price of silver being Rs.101 per tola, work out the dower? Mehar e Fatimee being 131.25 tolas of silver.
Question 5A school has 21 teachers, each receiving a salary of Rs.3500. Feeding expenditure of students is Rs.5000 per day. Electric and gas bills amount to Rs.2500 per month. An expenditure of Rs.200000 per year is incurred on construction. Rs.50000 are spent on purchase of new books for the library. Medicines for the students cost Rs.65000 per year. Beddings each costing Rs.225, have to be purchased for sixty students. Work out annual budget for the school.
Chapter 2- Fractions,Greatest Common Factor (GCF) and Lowest Common Multiple (LCM)
Fractions
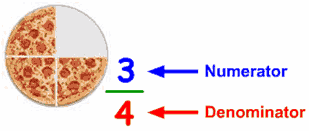
Part of a whole is called a fraction. If Rs. 2 have to be divided among four persons, each will receive less than a rupee i.e. 2/4. This is called 2 over 4. A number written with the bottom part (the denominator) telling you how many parts the whole is divided into, and the top part (the numerator) telling how many you have.
Equivalent Fractions
Some fractions may look different, but are really the same, for example:
4/8 = 2/4 = 1/2 (Four-Eighths) (Two-Quarters) (One-Half)

It is usually best to show an answer using the simplest fraction (1/2 in this case). That is called Simplifying, or Reducing the Fraction.
Proper and Improper Fractions
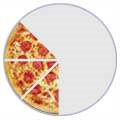
A Proper Fraction has a top numberless than its bottom number i.e. 3/8 (Three -Eighths)
Examples
3/8, 1/4, 14/15, 4/5
See how the top number is smaller than the bottom number in each example? That makes it a Proper Fraction.

7/4
An Improper fraction has a top number larger than (or equal to) the bottom number e.g.7/4 (seven-fourth or seven quarters)
Examples
3/2, 7/4, 16/15, 15/15, 99/5
See how the top number is bigger than (or equal to) the bottom number?
That makes it an Improper Fraction, (but there is nothing wrong about Improper Fractions).

1 3/4
A Mixed Fraction is a whole number and a proper fraction
combined. Such as 1 3/4 (one and three quarters)
Examples
2 3/8, 7 1/4, 1 14/15, 21 4/5
See how each example is made up of a whole number and a proper fraction together? That is why it is called a "mixed" fraction (or mixed number).
Greatest Common Factor (GCF)
The highest number that divides exactly into two or more numbers.
It is the "greatest" thing for simplifying fractions!

Greatest Common Factor is made up of three words
- Greatest,
- Common and
- Factor
Let us start with the last word:
What is a "Factor”?
Factors are the numbers you multiply together to get another number:
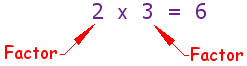
Sometimes we want to find ALL the factors of a number:
The factors of 12 are 1, 2, 3, 4, 6 and 12 ...
... because 2 × 6 = 12, or 4 × 3 = 12, or 1 × 12 = 12.
What is a "Common Factor”?
Let us say you have worked out the factors of two or more numbers:
Example:
The factors of 12 are 1, 2, 3, 4, 6 and 12. The factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30.
Then the common factors are those that are found in both lists:
- Notice that 1, 2, 3 and 6 appear in both lists?
- So, the common factors of 12 and 30 are: 1, 2, 3 and 6
Least Common Multiple (LCM)

The smallest (non-zero) number that is a multiple of two or more numbers is the LCM.
Least Common Multiple is made up of the words Least, Common and Multiple:
What is a "Multiple”?
The multiples of a number are what you get when you multiply it by other numbers (such as if you multiply it by 1, 2, 3, 4, 5, etc). Just like the multiplication table.
Here are some examples:
The multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, etc ... The multiples of 12 are: 12, 24, 36, 48, 60, 72, etc...
Example: Find the least common multiple for 3 and 5:
The multiples of 3 are 3, 6, 9, 12, 15, ...,
and the multiples of 5 are 5, 10, 15, 20, ..., like this:
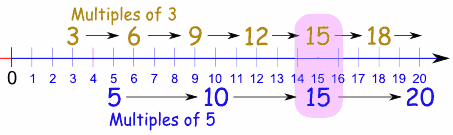
As you can see on this number line, the first time the multiples matchup is 15. Answer: 15
Addition of Fractions
There are 3 Simple Steps to add fractions:
- Step 1: Make sure the bottom numbers (the denominators) are the same
- Step 2: Add the top numbers (the numerators). Put the answer over the denominator.
- Step 3: Simplify the fraction (if needed).
Example 1
1/4 + 1/4
Step 1. The bottom numbers (the denominators) are already the same. Go straight to step 2.
Step 2. Add the top numbers and put the answer over the same denominator:
1/4 + 1/4 = (1 + 1)/4 = 2/4
Step 3. Simplify the fraction:
2/4 = 1/2
In picture form it looks like this:
1/4 + 1/4 = 2/4 = 1/2

(If you are unsure of the last step see Equivalent Fractions.)
Example 2
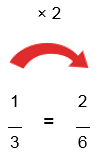
1/3 + 1/6
Step 1. The bottom numbers are different. See how the slices are different sizes?
1/3 + 1/6 = ?

We need to make them the same before we can continue, because we can't add them like that.
The number "6" is twice as big as "3", so to make the bottom numbers the same we can multiply the top and bottom of the first fraction by 2, like this:
Subtraction of Fractions
There are 3 simple steps to subtract fractions
- Step 1. Make sure the bottom numbers (the denominators) are the same
- Step 2. Subtract the top numbers (the numerators). Put the answer over the same denominator.
- Step 3. Simplify the fraction.
Example 1
3/4 – 1/4
Step 1. The bottom numbers are already the same. Go straight to step 2.
Step 2. Subtract the top numbers and put the answer over the same denominator:
3/4 – 1/4 = (3 – 1)/4 = 2/4
Step 3. Simplify the fraction:
2/4 = 1/2
Example 2
1/2 – 1/6
Step 1. The bottom numbers are different. See how the slices are different sizes? We need to make them the same before we can continue, because we can't subtract them like this:
1/2 - 1/6 = ?

To make the bottom numbers the same, multiply the top and bottom of the first fraction (1/2) by 3 like this:
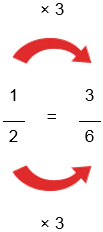
And now our question looks like this:
3/6 - 1/6
The bottom numbers (the denominators) are the same, so we can go to step 2.
Step 2. Subtract the top numbers and put the answer over the same denominator:
3/6 – 1/6 = (3 – 1)/6 = 2/6
In picture form it looks like this:
3/6 - 1/6 = 2/6

Step 3. Simplify the fraction:
Multiplication of Fractions
There are 3 simple steps to multiply fractions
- Multiply the top numbers (the numerators).
- Multiply the bottom numbers (the denominators).
- Simplify the fraction if needed.
Example 1
1/2 × 2/5
Step 1. Multiply the top numbers:
1/2 × 2/5 = (1 × 2)/ = 2/
Step 2. Multiply the bottom numbers:
1/2 × 2/5 = (1 × 2)/(2 × 5) = 2/10
Step 3. Simplify the fraction:
2/10 = 1/5
Division of Fractions
There are 3 Simple Steps to Divide Fractions:
Step 1. Turn the second fraction (the one you want to divide by) upside-down (this is now a reciprocal).
Step 2. Multiply the first fraction by that reciprocal
Step 3. Simplify the fraction (if needed)
Example 1
1/2 ÷ 1/6
Step 1. Turn the second fraction upside-down (it becomes a reciprocal):
1/6 becomes 6/1
Step 2. Multiply the first fraction by that reciprocal:
1/2 × 6/1 = (1 × 6)/(2 × 1) = 6/2
Step 3. Simplify the fraction:
6/2 = 3
Exercise 2
Question 1
Solve ½ + 3/5 -3/8+1/6+2/5-1/9+1/12-3/4.
Question 2In the budget of a school 6th is spent on salaries, 12th is reserved for the library, ½ is food and lodging and ninth is for the miscellaneous expenditures. After these expenditures Rs.40000 is saved. What is the total budget?
Question 3Wife of a deceased has received 1/8 share, his daughter ½ and 1/6 share was given to his mother. Remaining shares were distributed amongst the three paternal uncles as residuaries. Find out the share of each uncle.
Question 4Solve:
9/4÷ (7/2 – 5/8) 3 + 2/5 x7/9Question 5
Solve: 2/13 ÷ 5/26 x 2/3 ÷ 4/7 x ½
Question 6Two drums have 45 liters and 175 liters of oil in them. What should be the capacity of a container to measure the oil in both drums fully?
Question 7Three pieces of a rope are each 1365 cm, 910 cm and 1015 cm long. These are needed to be cut into equal lengths. What will the size of the cut rope?
Question 8Four different books are costing Rs. 78, Rs.60, Rs.50 and Rs.45 respectively. How much money will be needed to buy them all in equal numbers?
Chapter 3 – Unit Price Method
The "Unit Price" (or "unit cost") tells you the cost per liter, per kilogram, per pound, etc, of what you want to buy. Just divide the cost by the quantity. Saleem has purchased five books for Rs.40. What will be cost of eight books? Let’s first find out the unit cost of a single book 40 ÷ 5 = 8. Now to find the cost of eight books multiply 8x8 = 64. So the price of eight books is Rs. 64. This is the unit price method. Price of a single item is determined first and then it is multiplied by the required number of items. A problem is solved as:-
Price of 5 books = 40
Price of one book= 40/5 = 8
Price of 8 books = 8x8 = 64
Example 1
There is 10 days ration available for 8 students, how long will it last for 20 students?
Available ration for 8 students = 10 days
Available ration for one student = 10x8 = 80 days
Available ration for 20 students = 10x8 ÷ 20 = 4 days
Example 2
There was 30 days ration for 180 students in a religious seminary. With the induction of some foreign students the ration was consumed in 27 days. How many foreign students were enrolled?
Number of students to consume ration in 30 days = 180 students
Number of students to consume ration in one day = 180x30 students
Number of students to consume ration in 27 days = 180x 30/27 =200
Number of foreign students = 200- 180= 20
Exercise 3
Question 1
Saleem pays Rs. 7200 as three months rent. How much will he pay in a year?
Question 2A car travels 48 kilometers in 3 liters of fuel on an average. How much of fuel will be needed to travel a distance of 144 kilometers?
Question 3Price of 2/3rd part of a property is Rs.10000. Work out the cost of 3/4th of its part?
Question 4In a camp, there is 22 days ration for 600 mujahideen. After 10 days 200 more join in. How many days will the remaining ration last?
Question 5To determine the travel distance (masafat e qasar – 48 miles in plains) a scholar on an average travels 480 miles in 30 days. How much of Sharia distance is determined? Remember that Sharia travel distance conforms to average distance travelled in a day.
Question 6Arrangements for a congregation of 200000 have to be made. Experience shows that working on 1 1⁄2 feet of space per person, 15 persons can offer prayers between two poles. Fifteen rows are accommodated between the poles. Determine the number of poles and cloth needed?
Question 7Worth of the total property of a deceased is Rs. 1600000. Out of its 27 shares, 3 are given to the widow, each daughter receives 8 shares, and mother and father receive 4 shares each. Work out the sum received by each heir?
Question 8A person moving at a speed of 15 miles per hour on his bicycle reaches the destination in 1 ½ hours. How much time will he take to travel the same distance on a motor bike moving at an average speed of 45 miles per hour?
Chapter 4 – Percentage, Zakat and Loss & Profit
Percentage
Percent means parts per 100. The symbol is %. Example: 25% means 25 per 100 (25% of this box is green).
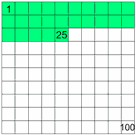
Example 1
100% means all.
Example:
100% of 80 is 100/100 × 80 = 8
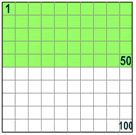
50% means half.
Example:
50% of 80 is 50/100 × 80 = 40
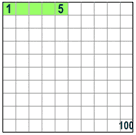
5% means 5/100ths.
Example:
5% of 80 is 5/100 × 80 = 4
A Percent can also be expressed as a Decimal or a Fraction

A Half can be written...
As a percentage: 50%
As a decimal: 0.5
As a fraction: 1/2
Example
In his Maths paper Wajid has secured 112 marks out of 150. Convert his marks into percentage.
Wajid’s marks out of 150 = 112
Marks out of 1 = 112/150
Marks out of 100 = 112/150 x 100 =83.63
Percentage of Wajid’s marks is 83.63%
Zakat (Obligatory Alms)
Zakat is one of the five basic tenants of Islam. Allah Almighty has laid lot of emphasis in the Quran on payment of the obligatory alms. It is mandatory for those who can afford it, to pay 2.5% of their holdings after a lapse of one year.
Example 1
A person had Rs.15000 for a year. How much zakat has to be paid?
Amount = Rs. 15000
Rate of Zakat = 2.5 %
Zakt = 2.5/100 x 15000 = Rs.375
Example 2
Wife of a person has in her possession Rs.6000 in cash, gold weighing 20 tolas and silver ornaments weighing 25 tolas. The person is under a debit of Rs.25000. However he has a plot worth Rs.200000 for making his house. How much zakat has to be paid by both?
Since both cash and ornaments are personal property of the wife, it is obligatory for her to pay zakat, irrespective of the loan taken by her husband. Both have to pay zakat separately. Plot being reserved for making own house is exempted from zakat. Zakat of the wife is:-
Value of 20 total gold @ Rs.5000/tola = Rs.100000
Value of 25 total silver @ Rs.100/tola = Rs.2500
Cash = Rs.6000
Total assets = Rs.108500
Zakat = 2.5/100 x 108500 = Rs.2712.75
Profit and Loss
In a business or else where if income is more than all expenses it is “profit” but if the income is LESS than expenses it is called a "Loss".
Example
Abid bought a washing machine for Rs.1400 and sold it for Rs.1000. Find out profit or loss?
Purchase cost = Rs.1400
Sold = Rs.1000
Difference = 1000 – 1400 = - 400
The difference with a minus sign indicates loss. Therefore loss incurred was Rs.400.
Loss & Profit in Percentage
In the above example we can find the loss in percentage.
400/1400 x 100 = 28.57
So the loss is 28.57 %
Exercise 4
Question 1
A person received 16 shares out of a total of 96 shares of inheritance. Find out the percentage of his shares?
Question 2Say in a taxation system, there is no tax on the first Rs.50000, then up to Rs.100000 the tax is 10%, then up to Rs.200000 it is 20 %, then up to Rs.400000 it is 25% and up to Rs.1000000 it is 30%. Find out the tax of a person whose income is Rs.700000?
Question 3Abdul Kareem has a plot (purchased for business) worth Rs.250000, a shop with stock worth Rs.900000, others owe him Rs.59000 and he has to pay a loan of Rs.246000. Find out his Zakat at the lapse of a year?
Question 4Shahid’s sister possesses 5 tolas of gold jewellery, 61 tolas of crafted articles of silver and Rs.11000 in cash. Rate of gold is Rs.3500 per tola and that of silver is Rs.95 per tola. Find out the amount of zakat to be paid?
Question 5Akram, Aslam and zubair shared a business with a ratio of 5: 3: 2. They decided to share the profit in the same ratio. Find out percentage share of each partner?
Question 6Zubair has two houses. He lives in one and the other has been rented at Rs. 2000 per month. At the end of the year he has a balance of Rs.31000 in his account. Find out his zakat?
Question 7To perform Hajj a person deposited Rs.80000, but could not be selected in the ballot. He kept the money for the next year. At end of the year he has a loan of Rs.2000 to pay. Has he to pay zakat? If the answer is in affirmative then how much? If it is no then why?
Question 8A fellow bought five cows at the rate of Rs.15000 per cow. He would sell 20 litres of milk daily @ Rs.15 per litre. After six months one of the cows died. He sold the remaining four cows for Rs. 48000.He had spent Rs.11000 on protection the cows. Determine his loss or profit?
Question 9A person stocked articles worth Rs.50000 in his shop. Being honest and straight, his reputation spread. After a year, value of the stock had increased to Rs. 71000. He had also been taking Rs.2000 per month for his domestic expenditure. How much profit did he make? Work out its percentage.
Question 10Tariq bought a piece of land for Rs.300000. He spent Rs.35000 on its registration. It was sold for 350000 after a year. How much profit did he make?
Question 11Muhammad Rafiq bought a house for Rs.1000000. He rented it for Rs.5000 per month. A sum of Rs.80000 was spent on repairs etc. He had to sell it for Rs.9500000 after a year. How much of profit or loss did he make?
Question 12A woman got five tolas gold ornament made for Rs.2000 excluding the price of gold which was Rs.3500 per tola. After five years she sold it back to the gold smith for Rs.3100 per tola. How much loss did she incur?
Question 13Junaid made a 20% profit in Rs.40000.Later he incurred a 5% loss but continued the business. Again he made a profit of 2%. Next year he made a profit of 31%. Work out his total loss and profit.
Chapter 5 – Ratio/proportion, Sharing, Mudar’ba and Averages
Ratio and Proportion
A ratio shows the relative sizes of two or more values. Ratios can be shown in different ways. Using the ":" to separate example values or as a single number by dividing one value by the total.
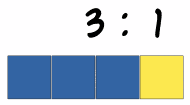
(There are 3 blue squares to 1 yellow square)
Anwar has two books and Khalil has four. Their books have a ratio of two is to four or 2: 4. Since both the numbers can be divided by 2, so we can simplify them and write 1:2. This shows that khalil has double the books than Anwar.
Example
A room is 20 feet long and 15 feet wide. What is the ratio between length and breadth?
Ratio of length and breadth = 20:15
Or = 20/5: 15/5
Therefore = 4: 3
Ratio in Fractions
Ratio can be expressed in fractions as explained above. In law of heritance an only daughter receives half the shares while 1/6 go to her mother. So their ratio is 1/2: 1/6. To simplify it further denominators of both fractions are multiplied with their LCM i.e. 1/2 x 6: 1/6 x 6 or 1:3. So the ratio between their shares is 1: 3.
Ratio of Continuous Numbers
Same method is used to find the ratio between more than two numbers. Only the ratio symbol (:) has to be added. E.g. Anwar has two books, Khalil has four and Rafiq has eleven books. The ratio therefore is 2:4:11 which can not be simplified any further being indivisible by a single number.
Ratio of Continuous Fractions
In presence of siblings, share of a wife is1/8, mother receives 1/6 and if a daughter is the only child she gets 1/2. Thus the ratio is 1/8: 1/6: 1/2. It is simplified further with the LCM method. So the ratio is 3: 4: 12.
Proportion
A proportion is an equation stating that two ratios are equivalent. The symbol used is “ :: ”.
Anwar has two books, Khalil has four, Rafiq has eleven and Fawad has twenty two books. Ratio between Anwar and Khalil is 1:2. Ratio between Rafiq and Fawad is 11:22 which is 1:2. Both these ratios being the same can be written as 2:4 :: 11:22.
One prominent characteristic of proportion is that multiplied product of the first and last item (extremes) and second and third (centrals) will always be the same. An unknown number in a proportion can be found e.g.
2 : 3 :: 4: k
Using the above, the multiplication product of the centrals 3x4=12, so product of extremes should be 2 x k = 12 or k= 12/2 or 6. Therefore value of K is 6.
Direct Proportion
If the ratio between two quantities changes by the same factor, they are in direct proportion e.g. Two quantities, A and B, are in direct proportion if by whatever factor A changes, B changes by the same factor. Less we buy the less we pay and more we buy the more we have to pay. Price of one kg of sugar is Rs. 60.Two kgs of sugar will cost 120 rupees and so on. With the doubling of the weight of sugar, its price has also doubled. Three kgs will cost Rs.180. So changing the quantity increases the price by a factor of 2.
Example
A labourer earns Rs.630 in 7 days. How much will he earn in 28 days?
Ratio in number of days is 7:28, so the earnings must have the same ratio.
Suppose he earns K rupees in 28 days i.e. 630:K.
Both ratios being the same, 7:28:: 630: K
Multiplication product of the extremes and centrals is 7 K and 28x630
Therefore
7 K = 28x630
K = 28x 630 ÷ 7 = Rs.2520
Inverse Proportion
When two quantities change by reciprocal factors they are inversely proportional. Two quantities, A and B, are in inverse proportion if by whatever factor A changes, B also changes by its multiplicative inverse, or reciprocal, of that factor.
Example 1
Five workers can complete a job in 4 days. How long will three workers take to finish the same job?
Number of Days Number of Workers 4 6 8 3
So 1/8: 1/4:: 3 : 6
Example 2
Driving at a speed of 60 km per hour a man reaches his destination in 4 hours. To reach in three hours, what should be his speed?
Inverse proportion in hours is 1/4: 1/3 and in speed it is 60: K.
Thus 1/4: 1/3:: 60: K
1/4 K = 60 x 1/3 = 20
Multiplying both sides of equation with 4
K =20 x 4 = 80 km per hour
Sharing
A few friends join in to start a business. Every one of them contributes equally or other wise. A business where more than one person share the capital is called a partnership. The sharers are known as partners. If all the partners have provided equal amount of money then they will all share the profit equally otherwise profit and loss will be shared according to the ratio of their investment. Expenditures are deducted before determining the profit. Sum total of the investment ratio of partners is called proportional sum e.g. sum total of 5: 4: 2 is 5 + 4 + 2 = 11.
Example
Abdul Rashid invested Rs.100000; Abdul Majid invested Rs.800000 and Salima Bibi gaveRs.150000 to start a partnership business. After one year after deducing the expenditure their total assets has increased to Rs.2150000. How much of profit will the each partner receive?
Total Investment = 1 + 8 + 1.5 = 10.5
Current value of Assets = Rs 21.5 Lacs
Profit = 21.5 – 11.5 = 10 Lacs
Share ratio = 1: 8: 3/2
Multiplying with LCM 2 = 2: 16: 3
Proportional Sum = 2 + 18 = 3 = 21
Share in profit - Abdul Rashid = 10 x 2/21 =20/21= Rs 95238.10
Share in profit – Abdul Majid = 10 x 16/21 = 160/21 = Rs.761904
Share in Profit - Salima Bibi = 10 x 3/21 = 30/21 = Rs.142857.14
Mudaraba (mazar’bat)
Mudaraba is Islamic partnership between investor and an entrepreneur in Islamic financing. A type of partnership in which one partner provides the capital while the other provides expertise and management services. Each gets a prearranged percentage of the profit. Losses are only borne by the partner providing the capital.
Abdul Rashid gave Rs.200000 to Amjad on the condition that Amjad will get 60% of the profit while Abdul Rashid will be given 40%. After one year they earned a net profit of Rs.100000. Out of it, Amjad will receive Rs.60000 and Rs.40000 will be given to Abdul Rashid.
The difference in mudaraba and partnership sharing is that in partnership the profit is distributed after deduction of salaries and expenditures in accordance with the ratio of investment. In a mudaraba, profit is divided according to the contract made between the financer and entrepreneur, irrespective of their number. In case of loss it is only borne by the financer/s (they share the loss if more than one).
Example 1
Wajid, Rafiq and Usman pooled rupees 50000, 18000 and 10000 respectively and gave it to Kamal for a business. It was decided that in case of profit Kamal will keep 60% and the rest will be divided in the financers according to the ratio of their investment. A profit of Rs.61000 was earned. How will it be divided?
60% share of Kamal = 61000 x 60 ÷ 100 = Rs. 36600
Remaining Profit = 61000 – 36600 = Rs.24400
Investment Ratio = 50000: 18000: 100000
Briefed Ratio = 5: 9: 25
Proportional Sum = 39
Wajid’s Share =24400 ÷ 39 x 25 = Rs.15641.03
Rafiq’s Share = 24400 ÷ 39 x 9 = Rs.5630.77
Usman’s Share = 24400 ÷ 39 x 5 = Rs.3128.20
Example 2
In example 1, a loss of Rs.2000 was incurred. How will it be divided?
In mudaraba, loss has to be borne by the financers. So it will be divided among the three investors.
Wajid’s Loss = 2000 ÷ 39 x 25 = Rs.1282.41
Rafiq’s Loss = 2000 ÷ 39 x 9 = Rs.461.54
Usman’s Loss = 2000 ÷ 39 x 5 = Rs.256.41
Average
A calculated "central" value of a set of numbers is called an average. It is easy to calculate. Just add up all the numbers, then divide them by how many numbers there are.
Example
What is the average of 2, 7 and 9?
Add the numbers: 2 + 7 + 9 = 18 and then divide these by how many numbers are there (i.e. we added 3 numbers): 18 ÷ 3 = 6
Example
In the adadia class there are 4 students aged 12, 14 aged 13 and 5 aged 14. Find their average age?
Total years of 12 year old = 4 x 12 = 48
Total years of 13 year old = 14 x 13 = 182
Total years of 14 year old = 5 x 14 = 70
Total number of student = 4 + 14 + 5 = 23
Total number of years = 48 + 182 + 70 = 300
Average Age 300 ÷ 23 = 13.04 years
Mean Value
In other words it is the sum divided by the count. The mean is just the average of the numbers.
Example 1
What is the Mean of these numbers 6, 11, 7?
- Add the numbers: 6 + 11 + 7 = 24
- Divide by how many numbers (there are 3 numbers): 24 / 3 = 8
The Mean is 8
Median
The Median is the "middle number" (in a sorted list of numbers).
How to Find the Median Value
To find the Median, place the numbers you are given in value order and find the middle number.
Example 1
Find the Median of {12, 3 and 5}
Put them in order: 3, 5, 12
The middle number is 5, so the median is 5.
Example 2
Find the median of 45, 36, 32, 39, 54, 50, 66, 44, and 47?

Example 3
In their maths paper four secured 80, 72, 64 and 32 marks. Find their median?

Since there are two central numbers, we will find their average i.e. is 72 +64 = 136 ÷ 2 = 68
So 68 is the median.
Exercise 5
Question 1
Continuous ratio of shares of heirs is 1/4: 1/6: 1/3: 1/3. Write it in simplified continuous ratio.
Question 2Find the value of L:
3: 8:: 2: L
A worker earns Rs.630 in 7 days. How much will he earn in 30 days?
Question 4Tariq and Khalid have a partnership with shares of Rs.10000 and Rs.20000. If Khalid earned a profit of Rs.3000. How much of profit will Tariq earn?
Question 5A mason can put 500 bricks in 4 hours. How many will he fix in 6 hours?
Question 6Divide Rs.900 between two brothers and a sister in a ratio of 2:1.
Question 7Zaid and Waqar contributed Rs. 50000 and Rs.70000 respectively to begin a business. A profit of Rs.24000 was earned. Determine their shares in the profit?
Question 8Ahmad and Zafar shared Rs.7500 and Rs.10000 in a venture. They suffered a loss of Rs.700. How much it will each bear?
Question 9Talal,Bilal and Miqal invested in a business. Their investment proportion is 1.5:2:3. Work out their shares in a profit of Rs.68000?
Question 10Shabbir gave Rs.50000 to Rafaqat for business. They had decided to share the profit in a ratio of 2:3. At end of the year they got a profit of Rs.51000. Find out per month profit of each?
Question 11Saleem provided a capital of Rs.80000 to Murad. It was decided to share the profit as 60% to Murad and 40% to Saleem. First year they suffered a loss and the capital was reduced to Rs.61000. Next year they earned a profit of Rs.21000. How much did each get?
Question 12Recorded temperature in Islamabad was; Saturday 39.72, Sunday 36.88, Monday 40, Tuesday 39.22, Wednesday 34.17, Thursday 29.44 and Friday 25.5 centigrade. What was the average weekly temperature?
Question 13Floor mats for a school were purchased as three mats for Rs.200 per mat, five at Rs.250 each and eleven for Rs.150 each. Find out the average price of mats?
Question 14Average of four numbers is 60. Find the fourth number other being 70, 50, and 55?
Question 15Average wages of a mason and six labourers is Rs.85. If average wages of five labourers is Rs.70 and sixth is Rs.75. What are the wage of the mason?
Question 16Fifty students on a yearly average graduated from a school for five years. In the sixth year another school was opened nearby. Only eleven students could pass out this year.Thirty graduated from the new school. What is now the average of the old school?
Question 17On a request of some eminent scholars, the new school was shifted else where. Next year 55 students passed out from the old school and 44 graduated from the new one. What is the passing out average of both the schools?
Chapter 6 - Graphs
General
A graph is a diagram of values or numbers, usually shown as lines or bars.
This pictorial expression of numbers/values is an effective tool for better understanding. To diagnose the type of fever of a patient, doctors usually ask the attendants to take temperatures with regular intervals and make a record. The record when graphically expressed makes it easy for a doctor to diagnose the exact nature of ailment. Graphs are being used virtually in every field of life to reach conclusions. These can be adequately used to gauge various aspects in religious schools, jihad and preaching etc. A graph can be used to prepare budgets, explain performance and educational aspects etc.
Type of Graphs
Line Graph
To make a line graph:-
Use the data from the table to choose an appropriate scale. All scales start at 0.
Draw and label the scale on the vertical axis.
Draw and label the horizontal axis. (Horizontal means "across
List the name of each item.
Locate the points on the graph.
Connect the points with line segments.
Write the title of the line graph
Example

Pie Graph
A pie chart is a circular chart divided into sectors; each sector shows the relative size of each value.
Bar Graph
A bar chart is a graph drawn, using rectangular bars to show how large each value is. The bars can be horizontal or vertical.
Double Bar Graph
A double bar graph is a bar graph with two bars that compare two sets of data.
Double bar graphs, also called double bar charts, help us to compare or present more than one kind of information, situations, or events instead of just one by using bars.
Histogram
A graphical display of data.
The data is grouped into ranges (such as "40 to 49"), and then plotted as bars.
Similar to a Bar Graph, but each bar represents a range of data.
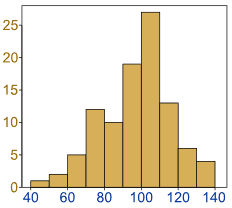
Exercise 6
Question 1
Relations of a sick person have prepared his temperature chart as shown below. Make a line graph.

Question 2
To explain the budget of a school, prepare a pie chart showing expenditures as; salaries 22%, construction 10%, books 5%, food 32%, furniture 6% and miscellaneous 25%.
Question 3Prepare a line graph where a volume is reducing by half every passing hour.
Question 4Make a line graph plotting time against a number which increases 10 times with every passing hour.
Question 5In a class, 3 students secured between 80 to 90 %, five between 70 to 80 %, ten between 60 and 70%, six between 50 and 60% and two secured between 40 and 50%. Prepare a bar graph expressing the result.
Question 6In question 5 above work out average marks to show the comparative result.
Question 7Based on the data in question 5, prepare line and bar graphs for comparison.
Chapter 7 – Power and Logarithms
Power
Definition
The power of a number shows you how many times to use the number in a multiplication.
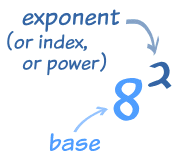
It is written as a small number to the right and above the base number. (Another name for power is index or exponent). A simple electronic calculator can solve the problems quickly.
In this example: 82 = 8 × 8 = 64
Examples
Exponents are also called Powers or Indices.
- In words: 82 could be called "8 to the power 2" or "8 to the second power", or simply "8 squared".
- In words: 53 could be called "5 to the third power", "5 to the power 3" or simply "5 cubed".
- In words: 24 could be called "2 to the fourth power" or "2 to the power 4" or simply "2 to the 4th"
Some more examples:
Example: 53 = 5 × 5 × 5 = 125
Example: 24 = 2 × 2 × 2 × 2 = 16
Exponents make it easier to write and use many multiplications
Example: 96 is easier to write and read than 9 × 9 × 9 × 9 × 9 × 9
So, in general:
an tells you to multiply a by itself,
so there are n of those a's:
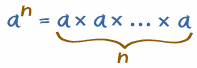
Inverse Power or Negative Exponent
A negative exponent means how many times to divide one by the number.
Example: 8-1 = 1 ÷ 8 = 0.125
You can have many divides:
Example: 5-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0.008
But that can be done an easier way:
5-3 could also be calculated like:
1 ÷ (5 × 5 × 5) = 1/53 = 1/125 = 0.008
In General
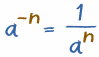
That last example showed an easier way to handle negative exponents:
- Calculate the positive exponent (an)
- Then take the Reciprocal (i.e. 1/an)
Exponent in Decimals
An exponent which is not a complete number but in between is called a decimal exponent e.g. If power of 9 is 2.5 then the answer is 243. Following two rules are
- Xm+n = Xm x Xn
- Xm-n = Xm ÷ Xn
Logarithm
How many of one number need to be multiplied to get another number.
Example How many 2s need to be multiplied to get 8?
Answer: 2 × 2 × 2 = 8, so we needed to multiply 3 of the 2s to get 8
so the logarithm is 3

In its simplest form, a logarithm answers the question:
How many of one number do we multiply to get another number?
ExampleHow many 2s do we multiply to get 8?
Answer: 2 × 2 × 2 = 8, so we needed to multiply 3 of the 2s to get 8
So the logarithm is 3
How to write it
We would write "the number of 2s you need to multiply to get 8 is 3" as
log2(8) = 3
So these two things are the same:

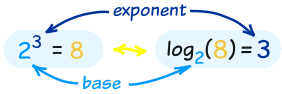
The number we are multiplying is called the "base", so we would say:
- "the logarithm of 8 with base 2 is 3"
- or "log base 2 of 8 is 3"
- "the base-2 log of 8 is 3"
Notice we are dealing with three numbers:
- the base: the number we are multiplying (a "2" in the example above)
- The number we want to get (an "8")
So when you have a question like this:
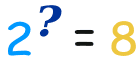
The Logarithm answers it like this:
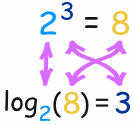
The logarithm tells you what the exponent is!
In that example the "base" is 2 and the "exponent" is 3:
Common Logarithms: Base 10
Sometimes you will see a logarithm written without a base, like this:
log (100)
This usually means that the base is really 10.
It is called a "common logarithm". Engineers love to use it.
On a calculator it is the "log" button.
It is how many times you need to use 10 in a multiplication, to get the desired number.
Example: log (1000) = log10 (1000) = 3
Natural Logarithms: Base "e"
Another base that is often used is e (Euler's Number) which is approximately 2.71828.

This is called a "natural logarithm". Mathematicians use this one a lot.
On a calculator it is the "ln" button.
It is how many times you need to use "e" in a multiplication, to get the desired number.
Example: in (7.389) = loge (7.389) ≈ 2
Because 2.718282 ≈ 7.389
So, be careful when you read "log" that you know what base they mean!
Look at some Base-10 logarithms as an example:
Exercise 7
Question 1
Find out 10 raise to power 2.5 i.e. 102.5 . Also prove that this is equal to the multiplication product of the square of 10 and its square root.
Question 2Find value of 63.1 ?
Question 3What is the equivalent of 5-3 ? Describe the working methodology.
Question 4Solve 101.4 x 107.1 x 101.5 .
Question 5Solve as logarithm 101.4 x 107.1 x 101.5.
Question 6Solve as a logarithmic problem 161/4.
Question 7Find out the natural log of 451.
Question 8Find out the natural log of 3.7985.
Question 9If question 3 is solved as a logarithm, what is exponent and which is the base?
Question 10Find the log of the desired number in question 4 of exercise 6 and then prepare its line graph against time (hours). What are your deductions?
Question 11Find the log of one light year i.e. 1000000000000 miles.
Chapter 8 – Taqwim (Conversion)
Background
The Islamic calendar is a lunar calendar consisting of 12 lunar months in a year of 354 or 355 days. Being a purely lunar calendar, it is not synchronized with the seasons. With an annual drift of 10 or 11 days, the seasonal relation repeats about every 33 Islamic years.
It is used to date events in many Muslim countries (concurrently with the Gregorian calendar), and used by Muslims everywhere to determine the proper days on which to fast in the month of Ramadan and perform Hajj, in addition to celebrate other Islamic holy days and festivals.
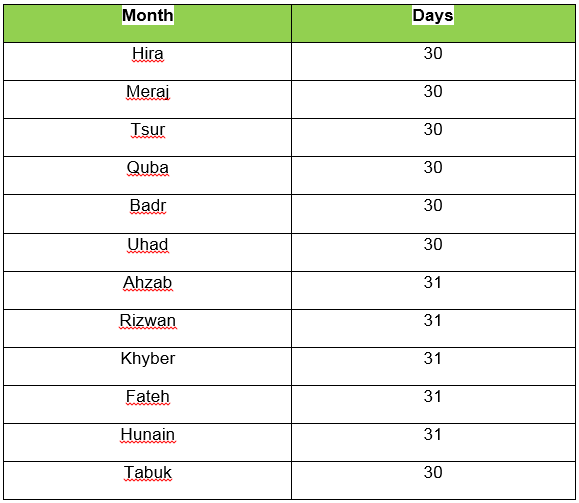
The first Islamic year began on 8 Rabi ul Awal, in 622 CE (Common Era, also Current Era or Christian Era is abbreviated as CE) when the holy Prophet Muhammad (SAW) migrated from Makkah to Madina, known as the Hijra. Each numbered year is designated either H for Hijra or AH for the Latin anno Hegirae (in the year of the Hijra. It is also called the Hijri calendar. First six months of Islamic calendar comprise of thirty days, next five are of 31days and the last month is the leap month of thirty one days.
Lunar dates cannot be pre determined because these are linked to the sighting of moon. However with a difference of one day or so these can be forecast.
Conversion from Gregorian calendar to Hijri Calendar
Hijri year = Previous CE years + number of days of CE year + 0.5 / 365 + leap – 621.54521
Lunar Hijri Year = Hijri year ÷ 09702248458247
If the Christian or civil year is a leap year put 1 for it otherwise put a zero.
To find the lunar Hijri year add one to the complete Hijri years, this will give the year. Multiply the fraction with 12. Add one to the figures on left of the decimal point. The resultant number will indicate number of the Islamic month i.e. 1 for Muharram , 2 for Safar, 3 for Rabīʿ al-Awwal, 4 Rabi al Sani, 5 for Jumādā al-Ūlā, 6 for Jumādā ath-Thāniya , 7 for Rajab, 8 for Shaban, 9 for Ramdhan, 10 for Shawal, 11 for Dhu al-Qa'da and 12 for Dhu al Hijja. Remaining fraction on left side of decimal point is divided by 29.530588. The answer will indicate the Hijri months. Add 0.5 to the left over fraction, complete number (ignoring fraction) is the converted date. One month will have to be added to the months to get number of the desired month. Similarly a year will have to be added to the years to find the desired year.
Example
Convert 7 May 2000 to Hijri date.
Previous years: 1999
2000 being a leap year: Add 1
No of days in 2000: 31 + 29 + 31 + 30 + 5 = 128
Hijri Year: 1999 + 128.5/366 – 621.54521 = 1377.80589
Lunar Hijri Year: 1377.80589 ÷ 0.9702248458247 = 1420.089266864
In the above equation 1420 is on left of the decimal point which is the lunar year. It being a leap year, figure 1 is added to actual lunar year 1420 + 1 = 1421 AH. Fraction right of the decimal point is multiplied by12 i.e. 0.089266864 x 12 = 1.07119968. Adding 1 on the left of the decimal point gives 2 which is the second month (Safar) of the Islamic year. Now multiply the fraction on right side by 29.53 (.07119968 x 29.53 = 2.102526). Here figure 2 indicates the date. Thus the complete answer is 2 Safar 1421 AH.
Lunar Calendar to Christian/Civil Calendar
Hijri Year = Previous complete Hijri years + complete months x 29.530588 + day + 8.5 / 354.367054
Civil year = Hijri year x 0.9702248458247 + 621.54521
Example
What was the civil date on 27 Ramdhan 1366 Lunar Hijri year?
Previous complete Hijri years: 1365
Complete months: 8
Previous days: 27
Hijri year = 1365 + 8x29. 530588 + 27 + 0.5 / 354.387054 = 1365.744269821426
Christian year = 1365.744269821426 x 0.9702248458247 + 621.54521= 1946.624233624
Adding 1 to 1946 is 1+ 1946 = 1947
Now multiply the fraction on right of the decimal point .624233624 x 365 = 227.8 days
Converting days into months 31+28+31+30+31+30+31(ignore fraction) is August i.e. 15 August. So 27 Ramdhan is 15th August 1947.
To Find Day of a Christian Calendar Date
Completed Days = Complete years x 365 + Year/4 – year/100 + year/400 + days of incomplete year.
This formula can be used to find the day occurring on a date of civil calendar.
After finding completed days divide it by 7. If the product is 1 then it is Monday, 2for Tuesday, 3 for Wednesday, 4 for Thursday, 5 for Friday, 6 for Saturday and 0 will indicate a Sunday.
Example
What was the day on 15 August 1947?
15 August = 31+28+31+30+31+30+31+15 = 227 days
Complete Days = 1946 x 365 + 1946/4 – 1946/100 +1946/400 +227 = 710988
710988 ÷ 7 = 101569 (with left over 5). So the day is a Friday.
Therefore 15th August 1947 was a Friday.
Conversion of Christian Calendar Date to Solar Hijri Date
Solar Hijri Calendar
The Solar Hejri year begins about 21 March of each Gregorian year and ends about 20 March of the next year. The Solar Hijri calendar produces a five-year leap year interval after about every seven four-year leap year intervals. It usually follows a 33-year cycle with occasional interruptions by single 29-year or 37-year sub cycles. The reason for this behaviour is (as explained above) that it tracks the observed vernal equinox. By contrast, some less accurate predictive algorithms are suggestion based on confusion between average tropical year (365.2422 days, approximated with near 128-year cycles or 2820-year great cycles) and the mean interval between spring equinoxes (365.2424 days, approximated with a near 33-year cycle).
Conversion Formula
Days of Complete Christian Year = Completed Year x 365 + year/4 – year/100+ year/400
Total Days (Christian) = Days of completed Christian year + Days of incomplete year
Total Days (Islamic Solar) = Total Days (Christian) – 227080
The above three formulas are used to first determine the Christian Days then to obtain
the Islamic solar calendar days. These days are then divided by 365.2422. Adding one
will give us the Solar Hijri Calendar century. In case of a leap year multiply it by 366
, otherwise with 365 to find the incomplete days of the year. Then find out the number of days in the respective from the table, one by one. When the left over figure is less than a complete month, it is the month and the numbers will indicate the date of Solar Hijri Calendar
Example
What will be the date of Solar Hijri Calendar on 9th May 2000?
Days of Incomplete year up to 9th May = 31+29+31+30+9= 130 Completed Years = 1999 Total Days (Gregorian) = 1999x365+1999/4-1999/100+130 Total Days Solar Hijri = 739249 – 227080 = 503169 = 503169 ÷ 365.24219878 = 1377.63106695
Here 1377 are complete years, adding one to it 1377+1= 1378 complete years.
Since 1378 is not a leap year so .63106695 x 365 = 230.33943675. Here total days of the incomplete year will be 230 because the fraction is less than 0.5. Now taking days of every month from the table, the 7th month Ahzab has only 19 days. So the date is 19 Ahzab 1378.
Conversion of Solar Hijri Calendar to Gregorian calendar
Formulas
Total days of Solar Hijri year = Complete year x 365 + year/4 – year/100+year/400 Total of Solar Hijri = Days of complete Solar Hijri Year + Days of Incomplete year. Total Days (Gregorian) = Total days of Solar Hijri + 227080
After finding the Gregorian total days with the help of these formulas these are divided by 365.24219878 and with addition of one, completed Christian years are found. If it is a leap year the remaining fraction on the right of the decimal point is multiplied by 366 otherwise (no leap year) by 365 to find incomplete days. After taking out the days of a calendar month one by one, the incomplete days will indicate the month and the leftover figure is the date.
Example
What was the Gregorian date on 1st Hira 1379?
Complete Years = 1378 Using above formulas, following are worked out:- Total days Solar Hijri = 503304 Totals Days = 503304 + 227080 = 730384 Christian Year = 730384 ÷ 365.24219878 + 1 = 2000. 72512059 Days of Incomplete year = . 72512059 x 366 = 265.3941360498
(Christian)
Since the fraction is less than 0.5, so 265 days will be counted. After month by month subtraction of days, 21 days in the 9th month are left. So the date is 21st September 2000.
Conversion of Solar to Lunar Hijri Calendar
Formulas
Total Days = Complete year x 365 + year/4 – year/100+year/400 + days of Incomplete year Total Days Lunar = Total days solar Hijri Calendar + 66
Hijri Calendar
After finding the total days with the above formulae divide it by 365.367054. Adding one to the answer will give century and the year. Multiply the decimal fraction with 12. In the answer, the digit on the left side of the decimal point with an addition of one will indicate the number of the lunar month. It may be named accordingly. The fraction on the right of the decimal point be multiplied with 29.53 and 0.5 added to the product. The digit/s on the left of the decimal point is the desired date. If it is more than 30 then change date to 1st and take the next calendar month.
Example
What will be the Lunar Hijri date on 1st Hira1379?
Completed years = 1378 Total days = 1378x365+1378/4-1378/100+1378/400+1+503305 Total days of Lunar Hijri = 503305 + 66 = 503371 = 503371 ÷ 354.367054 = 1420.47912
Digits left of the decimal point indicate the lunar year i.e. 1420. Multiplication of fraction right of the decimal point with 12 accrues 5. 749405. Addition of one with the digit left of the decimal point results in 6 i.e. the 6th month which is Jamadi us Sani. Fraction on the right when multiplied with 29.53 x 749405 = 22.12994 indicates the date. Addition of 0.5 makes no difference. So finally the date is 22nd. Thus the date is 22nd Jamadi us Sani 1421.
Conversion from Lunar Hijri Calendar to Solar Hijri Calendar
Formula
Total Days = Complete Hijri years x 354.367054 + full months x 29.530588+date+0.5.
After subtracting 66 from the answer, it is divided by 365.24219878. The digit on left of the decimal point with addition of indicates the year and century. In case of a leap year multiply fraction on the right with 366 otherwise with 365. After deducting the number of days in the calendar months one by one, the remainder days will indicate the current month and left days are the date.
Example
Convert 1st Shawal 1421of Lunar Hijri Calendar to Solar Hijri Calendar?
Total Days = 1420 x 354.367054+9 x 29.530588+1+0.5= 5033468.491972 = 5033468.491972 ÷ 365.24219878 = 1378.451048794 = .451048794 x 365 = 164.4 = 164-30-30-30-30-30 = 14
The date is14th of 6th month i.e. Ahad. So finally the date is 14th Ahad 1379.
Exercise 8
Question 1
Change following Gregorian dates to dates of Lunar Hijri Calendar.
4th October 1958, 8th November 1944, 6th September 1965, 17th December 1971, 5th April 726.
Convert the following Lunar Hijri dates to Gregorian dates.
17th Ramdhan 2, 1st Ramdhan 2, 10th Ramdhan 8, 9th Dhu al Hijja 9, 1st Ramdhan 1420, 1st Shawal 1420, 1st Ramdhan 1419 and 1st Shawal 1419.
Convert dates in question 1 to Solar Hijri Calendar.
Question 4Convert dates in question 2 to Solar Hijri dates.
Question 5Convert the following Solar Hijri dates to Civil (Christian) dates.
14th Hira 726, 10th Miraj 1120, 15th Sur 1002, 11th Tabul 922, 18th Ahad 832, 20th Badr 1210 and 11th Rizwan 1378.
Convert dates in question 5 to Lunar Hijri dates.
Chapter 9 – Islamic Law of Inheritance
Verses from the Holy Quran and the Hadith amply demonstrate importance of gaining knowledge about the Law of inheritance. It has been said that a scholar without this knowledge is like a head without face. So the subject is not optional but it is compulsory. It has to be learnt and acted upon lest loss in both the worlds is suffered. Muslim Laws of Inheritance have been made difficult by restricting their learning only to the terms and techniques used by our elders; totally ignoring their spirit. With passage of time, old mathematics has changed substantially, making it necessary to learn the new methods and techniques. In this chapter new techniques have been introduced to make the distribution of inheritance easy between the primary (obligatory sharers) and the secondary (residuaries) easy.
Terminology
Concept of Estate (tarka)
Any thing left behind by a deceased. After death it devolves on his/her legal heirs.
Real Brother (haqaqi)
Those of common parents (mother and father)
Consanguine Brother (allati)
Half brother (on father’s side) is one whose father is same as the deceased’s, but mother is different.
Consanguine Sister
Half sister (on father’s side) is one whose father is same as the deceased’s, but mother is different.
Uterinal Half Brother (Ikhyafi)
Same Mother.
Brother and Sisters (Ekhwa)
Two or more than two brothers and/or sisters. They may be real, consanguine, uterinal or a mix of the two.
Agnate Ancestor (jad e sahee)
A relative whose connection is traceable exclusively through males and no woman comes in between the relationship with the deceased e.g. paternal grandfather or a paternal great grandfather is the real ancestors.
Non Agnate Ancestor (jad e rehamee)
Here a woman is the link for relationship with the deceased e.g. a maternal grand father etc.
Real Feminine Ancestor (Jada Sahe’a)
In Arabic language a feminine ancestor (jada) is not restricted to paternal grand mother only. Any woman whose siblings are the parents of the deceased is a jad’a. A maternal grandmother falls in this category. However the real feminine ancestor is the one who has no female in lineage in relationship with the deceased. Mother of the grand father being the mother of the father of the father qualifies to be a Jada Sahe’a, but grandmother of the paternal grandmother cannot be included here being the mother of maternal grandfather of father of the deceased, is a false ancestor.
Obligatory/Primary Heirs (Dhawul Faruz)
Heirs specified in the Quran, hadith and by mutual consensus (ij’mah) to receive fixed shares of the estate e.g. half share of the only daughter (no brothers) of the deceased is laid down in the Quran. Sixth share of the real feminine ancestor is given in the hadith. Although they inherit first but generally do not take all of the inheritance
Blood and Casual Relationships (Dhawul faruz nasbi wa sababi)
Those relationships whose shares are laid down in Quran, Hadith and established through mutual consensus (ij’mah) because of circumstantial reasons are the casual heirs (dhawul sababi) e.g. share of a husband along with the children of a deceased woman is one fourth because of the matrimonial connections. It will cease as soon as the relationship ends. In the blood relationships of a common ancestor (dhawul faruz nasbi) those shares never cease e.g. share of a daughter. Unless one dies before the deceased or is involved in homicide i.e. the act of his/her murder accidentally or wilfully.
Explanation of off springs/Children
Only the male agnate children have the right to inheritance i.e. only those where a woman is not basis of the relationship e.g. son, daughter, grandchildren, great grandchildren and so on. With these relations present even the sisters and brothers of the deceased are disqualified. Only the mother will get a one sixth share. In case of non agnate children (where a woman connection is traceable) brothers and sisters of the deceased are not denied their shares. It also does not affect the shares of agnate off springs e.g. a great great grand daughter despite being a woman is the daughter of the son of the son of the son of the deceased and therefore an agnate relation. On the other hand a maternal grand son despite being a male is non agnate because of the feminine connection.
.Exclusion (Mahrum)
Sometimes an heir forfeits the right to his/her share because of an extra ordinary reason e.g. a homicide/ murderer and is denied the right of succession. Impediments to inheritance are personal acts or attributes which disqualify and individual from succession otherwise an entitled heir on the grounds of marriage or blood relationship to the propositus.
Reduced (‘awl)
If the fractional shares of agnate relations become more than one then the proportionate cut applied to complete the unit is called ‘’awl’. In this case all the agnate heirs receive less than their actual share e.g. ordinarily mother of the deceased gets 1/6th share but in the presence of daughters, wife and father share of the mother is reduced to 4/27th which is less than 1/6th share.
Residuaries or Secondary Heirs (asaba)
Successors by male agnate relatives of the deceased who are descendents through a male link from a common ancestor. They are entitled to the left over estate after the blood relations have taken their shares. It has been laid down in the Sharia. Details will be covered in the chapter on Assaba.
OR
Agnatic heirs or those who trace their relationship to the decedent only through males and take no fixed share but receive the residue after the fixed shares have been claimed by the primary sharers.
Heir by Special Reason (mauwla al ataq)
A person who releases a slave is called his mauwl al ataq. Inheritance of a deceased with no blood relations of a common ancestor is either give to his mauwl al ataq or his male agnate relative.
Return (Radd)
This is opposite of ‘awl (restriction). After distribution of the inheritance amongst the agnate relations, the left over estate is shared amongst the blood relations according to their proportions. This way their shares are increased.
Notation System of Fractional Proportions (se’ham)
Distribution amongst heirs is represented through fractional proportions (se’ham) e.g. shares of wife; mother and father of the deceased are given as 1:1:2. So it is said that wife gets one share, mother gets one and two shares go to father. Since proportion and unit are the same so if proportion of an heir is known then it is easy to work out the shares. To find out the share of a heir, divide his proportion over the total number of shares and multiply with the value of the inheritance. In the example quoted above proportion of wife is one out of a total of four se’hams. If value of the estate is Rs.2000 then:-
Share of wife:
1/4 ×2000=500
This is also called the unitary method.
Distantly Kindred Relations ( dhawul arham)
Those relations of the deceased who are neither blood relations from a common ancestor (dhawaul faruz) nor those in the category of assbat (succession by male agnate relations of the deceased). Some people think that a feminine link exists which is not right e.g. a paternal aunt is included in this category but her linkage with the deceased is through their father who is a male.
OR
More distant relatives of the decedent often called "distant kindred", who inherit if there are no sharers or residuaries.
Propositus (asal)
Propositus is person from whom a line of descent is derived on a genealogical table e.g. Zaid is descendents of Omar, so Omar is the propositus of Zaid, who becomes ‘farah’.
Agnate
Agnate is a relative whose connection is traceable exclusively through males.
Distribution of Inheritance amongst the Obligatory Shares-Primary Heirs (Dhawul Faruz)
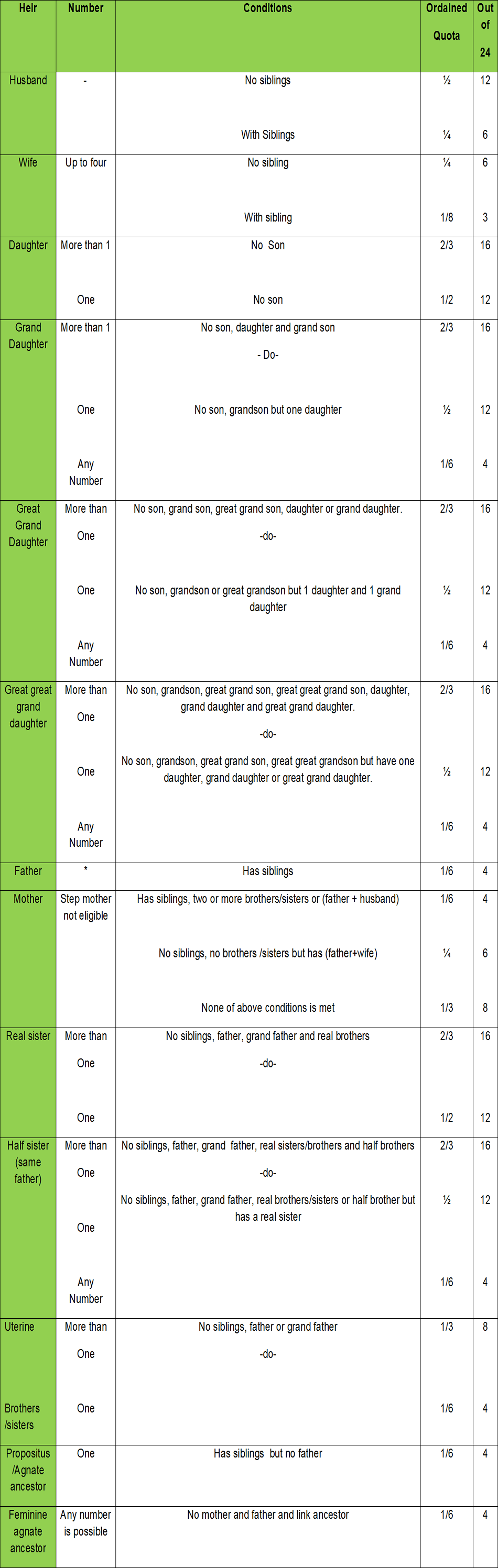
Table of Obligatory Sharers (primary heirs) given below has been prepared for this purpose. Explanations have added for use by Hanafi, Malikki and Shaffi jurists. Those of Hanbli School will need to modify it a bit. Definition of feminine agnate ancestor has been given in the glossary of terms. In this table it is mentioned that irrespective of their number they will receive 1/6th shares (4 se’hams) of the total estate less those excluded. In the residuaries genealogical tree shown, up to three generations of feminine ancestors have been listed. According to the table, if the mother is alive then all feminine ancestors are deprived of the heritage. A father or propositus only deprives the agnate feminine ancestors. A propositus, however, can not deprive those who do not form the link between the deceased and them e.g. a grandfather cannot deprive a grandmother being his wife but he deprives a great grandmother because he forms the link with the deceased. Only one generation of feminine ancestor can inherit and that has to be the nearest one. This means that nearer generation disqualify the older ones. They themselves could also get excluded for some other reason e.g. between the father, grandmother (paternal) and mother’s grandmother, the paternal grandmother excludes the mother’s grandmother despite being excluded herself because of the father. A feminine ancestor of multiple relations i.e. being both paternal and maternal grandmother of the deceased will only receive one fixed shares for a feminine ancestor.
Table of Primary Heirs
Solution of Problems- Primary Heirs
Rule1 (A)
If total of the fixed shares comes to 24 or more and number of heirs is one or even if more than one but their shares get equally distributed then no change is required to be made.
Example 1
Rashid left behind two daughters, a mother, a father and a paternal grandmother. Determine their shares?
According to the table of primary heirs, Rashid’s mother and father will receive four shares each because the deceased has left behind siblings. Rashid’s grandmother will be excluded because of the father and mother. Two daughters together will receive 16 shares because no son exists. Dividing the total by 2, each daughter will get 8 shares. Rest of the shares will remain the same as shown in the table.
Rule1 (B)
Number of heirs in a certain category is more than one and their total fixed share is not equally divisible. Find out the LCM of their total number and multiply this with shares of all heirs and then divide it on their respective numbers. Also multiply the LCM with the total number of fixed shares to accrue the corrected values.
Example 2
Increase number of daughters to three in example 1.
In example 1 total number of fixed shares for the daughters is 16, which is not equally divisible by 3.Now multiply all the fixed shares by 3 and divide it on their respective numbers. LCM of 1and 3 is 3. So the shares will workout to be; father 12, mother 12 and daughters’ 16 each.
Example 3
On his demise Abdul Sami, left behind three daughters, mother, father and two wives. Find out the share of each?
According to the table of primary heirs two wives will collectively receive 3 shares because the deceased has siblings. Daughters will together get 16 shares because of their number being more than two and absence of a son. Mother and father will receive 4 shares each because deceased has siblings. Total of their shares comes to 3+16+4+4=27 which is more than 24. According to rule 1 this make their shares. Since the number of wives and daughters is more than 2 so find out the LCM which is 6. Multiply all fixed shares by 6 and divide it by their number in each category:-
Wife: 3x6/2=9 Daughter: 16x6/3=32 Mother and Father : 4x6 = 24
Note. When the total of shares increases from 24, shares of each category of heirs gets reduced (‘awl) than usual. Application of the above method will automatically bring in the requisite correction without even knowing the ‘awl.
Rule 2
If the sum total of the shares of the primary heirs is less than 24 then subtract the total from 24 and distribute the remaining shares amongst those residuaries (asbat) who are nearest to the deceased. (Also see the lineage tree of residuaries). If all residuaries are males or females only then divide them equally otherwise in a mix a male will get double the share of a female. To solve such problems easily convert a male into female, add the number of females to it. You will get all female residuaries. Now divide the residuary share to get share of each female. To work out the male share simply double it. Rest is according to rule 1.
Explanation of Residuary Tree of Lineage
This tree shows the details and sequence of the residuaries or secondary heirs (al assbat). They are entitled to the shares left over by the primary heirs. In this tree, there are 78 code numbers. To determine the eligibility check the code number of heirs. Ones with the lowest code number become eligible to inherit the leftover estate and property. Others stand deprived. This rule is based on “Al aqrab fa la aqrab”. Heirs with the lowest code are nearest to the deceased so more deserving. All heirs in one code according to jurists have a similar relationship with the deceased.
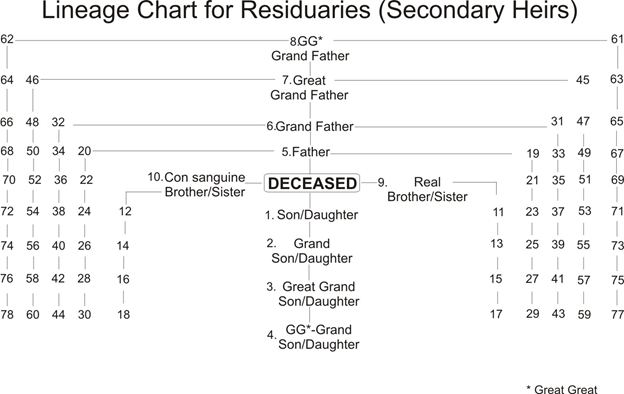
Chart of Real Feminine Ancestors
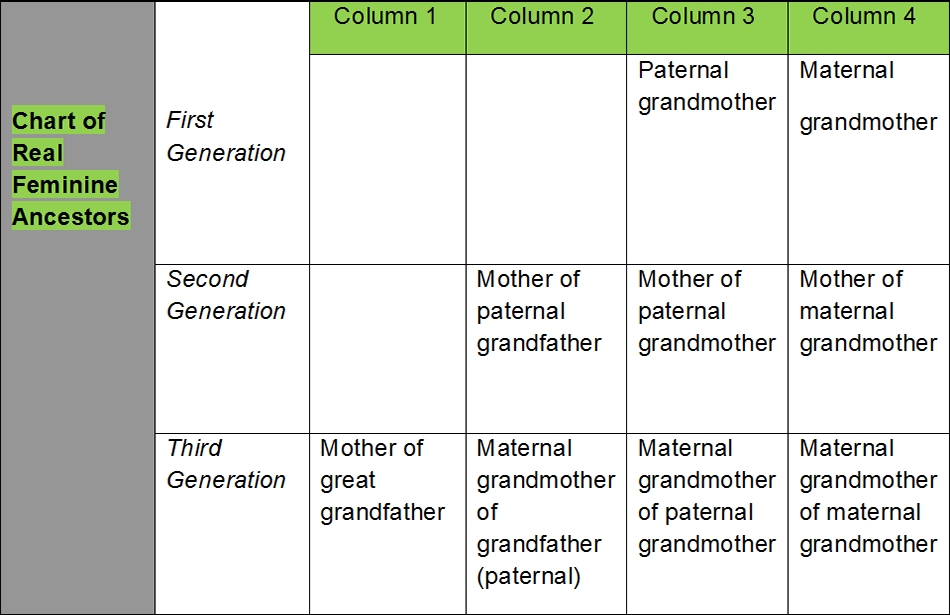
Only those women excluded from the primary heirs can participate in the residuary heritage. Women get a share only when they have a male sibling as a direct descendent or in the next generation (Tasbeeb). In the presence of more than one real sister, half sisters are deprived but half brothers are included in the residuaries. Those with the lowest code are nearest to the deceased as such eligible residuary heir. Amongst them if they all males or females, inheritance is equally divided otherwise a male gets double the share of a female.
Conditions laid down in this table relate to the deceased. Siblings mean the children/grand children of the deceased. Those eligible as primary or residuary heirs are son, daughter, grandson and great grand daughter etc. Maternal grand children are not eligible being non agnatic relations. The Propositus /Agnate ancestor (real) is the one where no female linkage exist e.g. paternal grandfather or great grandfather. Maternal grand father is a false ancestor because mother of the deceased is a female.
The real feminine ancestor is the one who does not have a female link e.g. Mother of maternal grandfather is a false ancestor but mother of the paternal grandfather is a real feminine ancestor. In the table of real feminine ancestors those in the third and fourth column are considered real ancestor by Maliki School. Those in the second, third and fourth column are real ancestors in Hanbli religion, whereas Hanfi and Shafi Schools consider all in the four columns as real feminine ancestors.
Easy Method for ‘Lilzikr Misal hiz ul Unsyan’ Claculations.
These calculations are needed while working out the shares of secondary heirs (assbat) and distantly kindred relations (dawul arham). Correction of shares becomes easy through this method. According this Quranic Rule males get twice the share of a female. Double the strength of males and add the number of females into it i.e. convert males into females for distribution of shares left form the secondary heirs. If they are equally divisible then a male gets two times the share of a female. If the total is not divisible then apply Rule 1 of the primary heirs i.e. LCM method.
Example 4
Abdul Basit left behind a wife, three daughters, one grand daughter, a great grand son, two great grand daughters, two great great grand sons and three great great grand daughters. Find out their shares?
According to the table of primary heirs wife will get 3 shares, daughters will receive 16 shares because the deceased had no son. In the remaining 5 proportions granddaughter gets excluded because of the absence of a grandson. In male siblings of the deceased great grandson (GGS) a great great grandson (GGGS) are alive. Code of great grandson is 3 where as that great great grandson is 4, so they get excluded.
Great granddaughters (GGD) are combined with great grandsons being in the same code number. In accordance with the concept of “tasheeb” granddaughter (GD) is also included. Remaining five shares have to distributed between a great grandson, two great daughters and the granddaughter. Great grandson being a male gets twice the share or shares of two women totalling to five women share. So GGS gets two shares, each GGD and GD one each. Shares of Abdul Basit’s three daughters come to 16 which is not equally divisible. Supposed number of residuary females is 5, every female getting a single share. LCM of 1and 3 is 3. Working according to Rule 1 we get the following:-
Wife: 3x3/1 = 9 Daughters: 16x3/3= 16 Residuary females (GGD): 1x3/3=3 GGS: 3x2=6
Example 5
Abdul ul Jalil left behind a mother, a wife, grandfather and great grandfather. How many shares will they get?
Mother of Abdul ul Jalil will get 8 shares in the absence of siblings (aulad e akhu) and his wife will receive 6 shares. The grandfather will be excluded from the primary heirs because the deceased had no siblings. Total shares of the primary heirs are 14.Rest of the 10 shares will be distributed amongst the secondary heirs (residuaries). Now amongst the residuaries code no of the grandfather is 6 and that of great grandfather is 7.Since grandfather has a lower code all the 10 leftover shares will go to him.
Code 9
This code covers the real brothers and sisters of the deceased. In the absence of relations at code 8 heirs at code 9 become eligible. If there are only males or females then estate is equally divided amongst them. In a mix men get double the share of a woman. A different treatment is meted out to the real sisters. Unlike granddaughters or great granddaughters they do not need a an equal or lower male connection to be eligible for the left over estate as a secondary heir.
Code 10
This code covers the half brothers and sisters (Consanguine) of the deceased. In the absence of relations at code 9 heirs at code 10 become eligible. Amongst heirs if there is only one real sister and there are only males or females then estate is equally divided amongst them. In a mix men get double the share of a woman. In case of more than one real sister as a primary heir, half sisters can only become eligible if the deceased has a consanguine half brother. Otherwise they will become ineligible and right of inheritance will shift to those covered under code 11.
Code 11
This covers real nephews of the deceased. This and codes above it are for the male heirs. In case of a single male heir he receives all the remaining estate. Otherwise it is equally distributed.
The Chart of lineage for residuaries covers up to four generations only. If needed, it can be extended further. To extend the lineage beyond the great great grandfather keep on extending an ancestor/ propitious linking it on both sides through vertical lines with his brothers. Then create chart of siblings of brothers like a tree in a lineage chart. Keep on numbering them in accordance with the existing code. The chart can be extended to any level. It is advisable to conform to the coding system.
Example 6
On his demise, Abdul Hamid left behind a wife, mother, a real uncle, and two real nephews (consanguine). Find out their shares?
His wife will receive six proportional shares and eight will be for the mother (In absence of siblings, brothers and sisters and father). Remaining 10 shares should be distributed amongst the uncle (code # 31) and the nephews (code # 12). Being in the lower bracket the nephews will receive all the shares i.e. five each.
Brevity Method/ Simplication
This method can provide corrected answers. Proportional shares of all heirs should be divided by a common denominator to lower their value. Keep on dividing them by the lowest number till they all get divided by a single digit.
Example 7
Abdul Jabbar left behind two wives, a mother, two daughters and three sons. Divide his inheritance amongst the heirs.
After giving 3 proportional shares to wives and 4 to mother, 17 shares are left. In the presence of sons, daughters are excluded from the primary heirs. Now the remaining shares will have to be divided according to ‘Lilzikr hiz ul Unsyan’. Keeping in mind that a male gets twice the share of a female, so converting sons to daughters we get a figure of 6. Add 2 into it. Sum total is 8. Let’s call it Sum A. Since17 cannot be divided by 8, let’s suppose 17 to be the proportional share of a daughter. Two sons thus receive 34 shares. Wives get 24 because they previously had 3. 3x8=24. Mother had 4.So her shares now become 4x8=32. Sum total of all the shares previously was 24. So 24x8=192. Two wives have 24 shares which is divisible by 2. So wives will receive 12 shares each, mother 32, each daughter 17 each and every son will receive 34shares.
Rule 3 (Reduction)
If sum of proportional shares of the primary heirs is less than 24 and no residuaries exist then remaining shares will be distributed amongst the blood related primary heirs (dawul farzi nasabi) according to proportions laid down for them. An easy method is as under:-
- a. If casual primary heirs are not there then while maintaining the laid down proportion of distribution, estate is divided amongst the blood related primary heirs in accordance with their number.
- b. If casual primary relations exist then:-
- Find the sum total of blood related primary heirs and call it ‘X’.
- Subtract the proportional shares of casual primary relations from 24 and call it ‘Y’.
- Now multiply X with the sum of the shares of casual primary heir and multiply Y with the sum of the shares of the blood related primary heirs. You will get shares after application of ‘reduction’.
- Considering the total shares to be 24 multiply it with X to find the total shares after reduction.
Rule 3 - Alternate Method
If casual primary heirs (CPH) are present:-
- Based on the ratio of fractional shares of CPH find its sum.
- Multiply the sum with the denominator (makhraj). Subtract the number of shares of CPH from it.
- Divide the result obtained from subtraction according to their laid down proportion.
Example 8
Muhammad Zubair left behind a wife, mother and a daughter. Find out their shares?
Wife gets 3shares, 4 go the mother and daughter receives 12 shares. Total of distributed shares comes to 3+4+12=19 which is less than 24. No residuaries exist to claim the remaining 5 portions. So these have to be reduced to the mother and daughter. The shares of blood related primary heirs are 4+12=16. Let’s call it X. Subtracting 3 shares of the wife from 24 comes to 21. Call it Y. Multiply the shares of the wife (casual primary heir) with X. 4x16=48. Multiply the shares of mother and daughter with Y. Mother (4x21=84) and daughter (12x 21=252). For the sake of ease brevity method is adopted as shown in the table below. Divide the proportional shares by the lowest common divisor i.e. 2. Keep on dividing them till they are divisible. Then divide them by the next lowest common divisor which is 3. Distribution of shares will be; wife 4, mother 7 and daughter will receive 21 shares.
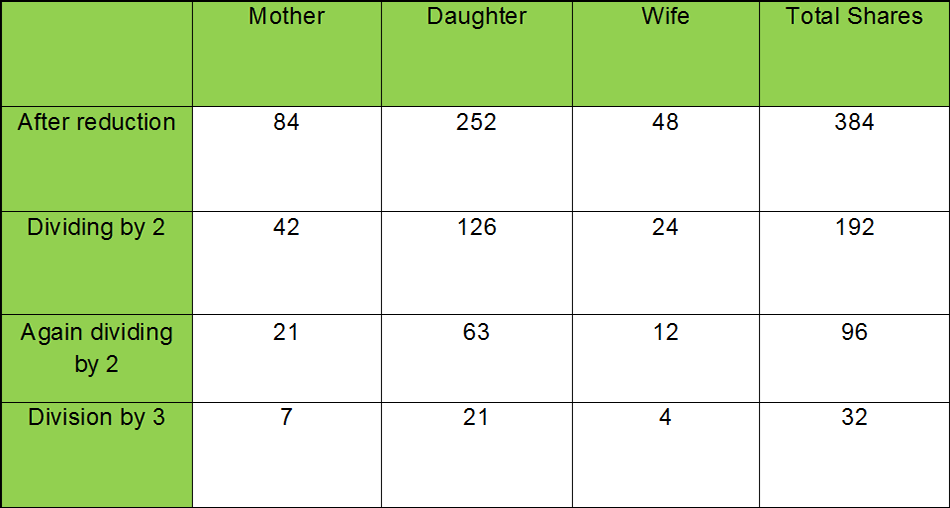
Alternate Method
Mother receives 1/6, daughter ½ and wife 1/8. Mother and daughter being blood related primary heirs the ratio of their shares have a ratio of 1/2: 1/6 or 1:3. Their total sum comes to 1+3=4. When multiplied with denominator of wife’s fraction i.e. 8 (4x8=32). These are the total shares for distribution. Out of these wife will receive (32x 1/8=4).Left over 32-4=28 are left for distribution amongst the blood related primary heirs. In accordance with the ratio of 1:3 mother will receive 28x1/4=7 and 28x3/4=21 shares will
Distantly Kindred Heirs (Dhawul Arham)
According to Hanfi School of Jurisprudence, distantly kindred heirs are treated like the residuaries / secondary heirs (asabat) as…………. (hajib mhjub). Details are being covered in tables 2 and 3. All types of inheritance problems can be easily solved with these tables. Be it method of Imam Abu Yousaf (RA) or Imam Abu Muhammad (RA).
In Table 2 gender number, code and group numbers are given. With help of this table first thing is to find out the gender, code and group numbers of the existing heirs. In case of a reference to the siblings as Sibling 1, Sibling 2 and Sibling 3 consult Table 3. In Table 3 every code has been assigned a degree number also. Remember the following rules:-
- LDK. Law of distantly kindred heirs.
- LDK 1. Those with lower gender number. Only they can participate. Rest are ineligible
- LDK 2. Those with lower degree. Only they can participate. Rest are ineligible.
Method of Imam Abu Yousaf (RA)
After selecting the heirs in accordance with LDK 1 and LDK 2, if their gender numbers are 1, 2 and 3; only those with the lowest number are eligible. In case of all males or all females being present, the estate is equally divided between them. In a mixed group, a male gets twice the share of a female (Liz zikr misl hifzul unsayn).
If the heirs are from Gender # 4 and include parents and relatives from both paternal and maternal sides then maternal relatives receive 1/3 rd of the leftover estate. Paternal relations will get 2/3. In case of absence of relations from either of the side, those present from the other side will receive the remaining estate.
Method of Imam Abu Muhammad (RA)
Following LDK rules, chose the eligible heirs with lowest numbers from both the tables. Consult Table 4 and follow the instructions.
Table 2
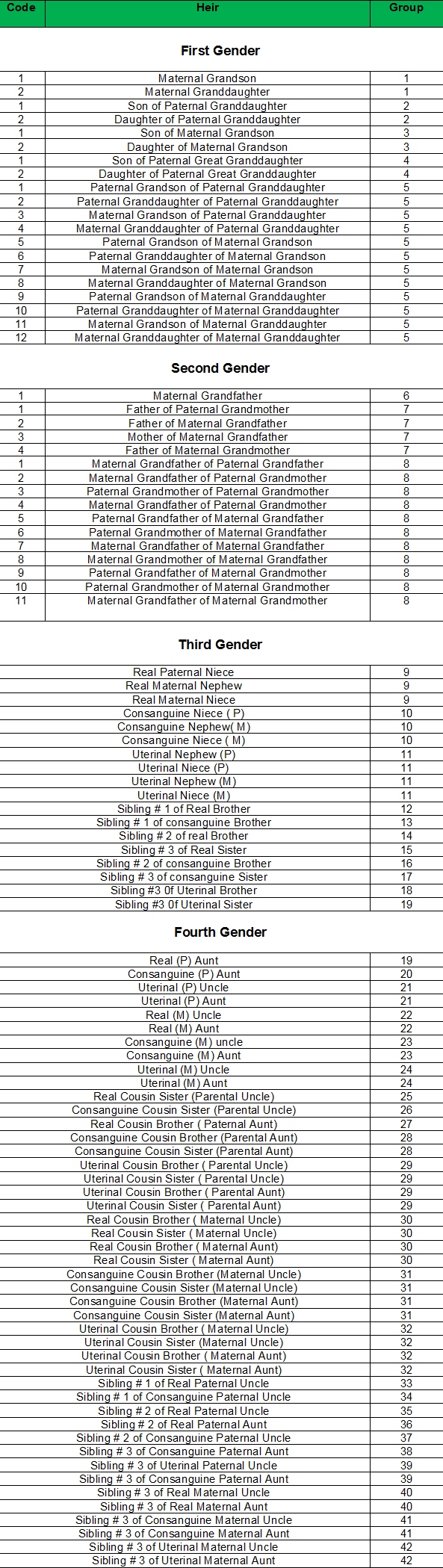
Note: Explanations of Siblings 1, 2 and 3 are explained in Table 3 below.
Table 3
Note: Siblings #1are actually the primary heirs. Siblings # 2 are only distantly kindred. Where as Siblings # 3 are a mix of the two.
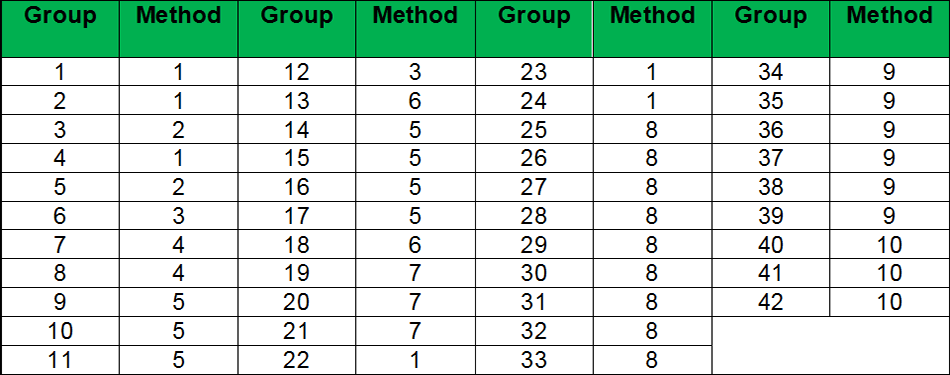
Method 1
Only those with the lowest number are eligible. Rest are to be excluded. If there are only males or females then estate is divided equally otherwise in a mixed group, a male gets twice the share of a female. See question # 1 for explanation.
Method 2
- While keeping the heirs with the lowest number, delete the rest. Arrange the eligible heirs in sequence of their code numbers starting from the lowest. Also mention their total number (strength) against each.
- As shown in example 1, write down the relationships in front of each heir e.g. In front of the maternal grandson of maternal grandson is written daughter, son, daughter and son. Write males and females separately. Number the emerging columns.
- Repeat the same procedure for the next generations and keep on numbering them. In a generation where both males and females are present separate columns are made and numbered. As shown in example 1, in the siblings of column 1, there are two more columns i.e.2 and 3.
- If a column shows only one type of descendants then no further columns are added irrespective of existence of mixed gender subsequently. See example 1, column 1.
- If the children of the deceased or those of subsequent generations are single gendered then make only one column and give it a value of 1. In case two columns are to be made, value of male column will be twice that of the female column. Adding the two will give the total value (weight age). Dividing the value of each column with the total value will give fractional value of each column. In example 1, there are two males in column 2 who represent the two maternal grandsons. So they will be assigned a value of 2x2=4. Value of column as such is 4. In column 3 there are 3 females thus the value of the column is 3. Cumulative value of columns 2 and 3 is 4+3=7. Dividing each value gives fractions of 4/7 and 3/7.
- Once all the columns have been completed, make a table and write down the fractional values. To find the share of an heir, multiply the fractional value with the corresponding column
Example 1
Distribute the estate between two maternal grandsons of maternal grandsons, a paternal grandson of a maternal granddaughter, maternal grandsons of two maternal granddaughters and one real maternal niece.
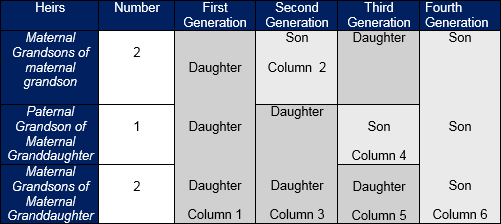
Solution
All the four are distantly kindred heirs. According to Table 2, except for the real maternal niece, other three are listed in the First Gender, while she is in the Third gender. According to DKL 1 she stands excluded. The selected heirs are from group 5 and degree 3, so they are eligible.
As indicated in Table 4, Method 2 has to be applied here. After finding code numbers from Table 2 make the table as shown above. Make fractions as under.

Column 2 is about a single heir so no further columns will be inserted. Column 3 lists more than one heir so more columns can be made for siblings. Columns 4 and 5 are inserted without changing the gender. Son listed in column 4 will be assigned a value of 2, where as girls at column 5 will have a cumulative value of 2. Their fractions thus are 2/4 and 2/4.
Now at this stage mark the columns from where an heir is receiving shares. Sum total of fractions after multiplication will indicate their share. Two maternal grandsons of maternal grandsons are receiving their shares from columns 1, 2 and 4 with fractional value of 1, 4/7 and 1. After multiplication 1x4/7x1= 4/7. Each will get 1/2x 4/7=2/7. Paternal grandson of maternal granddaughter receives his shares from columns 1, 3 and 5. Thus 1x3/7x2/4=8/28. Maternal grandsons of the two maternal granddaughters are receiving their shares from columns 1, 3 and 6. So 1x3/7x2/4=6/28=1/2x6/28=3/28.
Method 3
Maternal grandfather being the only eligible heir receives all the remaining estate.
Method 4
The only difference from Method 2 is that here males means fathers and females as mothers, whereas in Table 2, sons and daughters were implied. Columns made here will indicate mothers and fathers respectively. No fractions have to be calculated as these are already fixed; father receives 2/3 and mother 1/3. Number of an heir is one only.
Example 2
Find out the shares of father of paternal grandmother, father and mother of maternal grandmother and maternal grandfather of maternal grandmother.
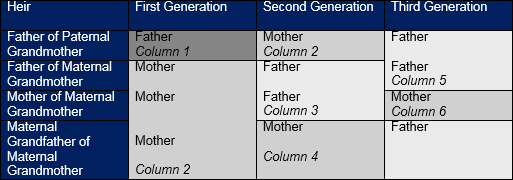
According to Table 2, all the heirs being in the third gender are eligible. The first four are listed in group 7 and maternal grandfather of the maternal grandmother is in group 8. So according to the proximity criterion of ‘ila aqrab fala aqrab’ he stands excluded. All the eligible heirs are tabulated according to their code numbers as shown in example 1. All being single, the number row is omitted in the table. In accordance with Method 4, make separate columns for males and females. Columns 1, 3 and 5 being columns for fathers (male) have a fraction of 2/3. Whereas columns 2, 4 and 6 are for mothers (female) with a fraction value of 1/3. Father of paternal grandmother is receiving his share from column 1 with a fraction value of 2/3. As such this is his share. Father of maternal grandfather receives his shares from columns 2, 3 and 5 (1/3x2/3x2/3=4/27). So his share comes to 4/27. Following the same method shares work out to be; mother of maternal grandfather (1/3x2/3x1/3=2/27), father of maternal grandmother (1/3x1/3=1/9).
Method 5
In this method all participants are considered as their ancestors because they mostly are the brothers and sisters of the deceased. Shares received by them as primary and secondary heirs will therefore determine shares to be given to their siblings in accordance with Methods 1 and 2.
Example 3
Distribute estate between three maternal grandsons and two maternal granddaughters of real brother of the deceased, two paternal grandsons and one maternal granddaughter of the real sister (agnate), one paternal grandson of consanguine sister and paternal grandson of the uterinal brother.
In this example, the real brother has five, real sister three, consanguine sister one and uterinal brother one descendant. Following Method 5, let’s suppose that estate is to be distributed between five real brothers, three real sisters, one consanguine sister and one uterinal brother. In the presence of the real brothers the consanguine sister is excluded but the uterinal sister will receive four out of the 24 share (se’hams). Remaining 20 shares will be given to the real brothers and sisters as residuaries following (Liz zikr misl hiz ul unsyn). Converting brothers to sisters we have a total of thirteen sisters (5x2+3=13). Since 20 is not equally divisible by 13, so let’s suppose that each sister will receive 20 shares. Brothers will therefore receive double the share i.e. 2x20=40. Now according to the rule the uterinal sister will now receive (13x4=52) shares thus making a total of 13x24=312 shares. These will be given as real brothers 40 each, real sister 20 each and uterinal sister 52.
Let us now distribute the shares of the real brothers between their siblings; three maternal grandsons (MTS) and two maternal grand daughters (MTG). In table 2, these siblings are listed in group 1. According to Table 3, method 3 will be applied here (Liz zikr misl hiz ul unsyn). Converting males into females makes 8 MTGs. Forty shares of the real brother will divided as 40/8=5. So a MTS will get 5x2=10 shares and MTG will receive 5 shares each.
Method 2 will be applied to distribute shares of the real sister between her siblings i.e. two paternal granddaughters and a maternal grandson. Make the table as shown below.
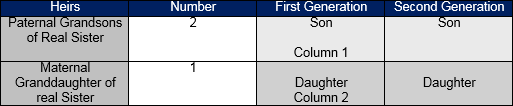
Since there is a change of gender in the first generation, two separate columns will be drawn. Fractional values of these columns are 4/5 (column 1) and 1/5 (column 2). If a column is only related to a single heir no further column will be made. It will remain the same till the very end. In this example no more than two columns can be made. Paternal grandsons receive their shares from column 1 so their individual share is 4/5 x1/2=2/5. The granddaughter will receive 1/5 shares from column 2. So out of the 20 shares of the real sister, grandsons will receive 20x2/5=8 shares each and granddaughter will be given 20x1/5= 4 shares. Paternal grandson of the uterinal sister will receive all of her 52 shares.
Method 6
This method only relates to uterinal brothers and sisters. So estate will be divided equally between them.
Method 7
- If both paternal and maternal relations are present then 2/3 of the remaining estate will be shared by the paternal relatives and 1/3 will be given to maternal relations. In case only one side is present then whole of the remaining estate will be divided amongst them
- In both categories of relatives, those in the lower group will receive shares. In case of there being only males or females; it will be distributed equally otherwise a male shall receive twice the share of a female (Liz zikr misl hiz ul unsyn).
Example 4
Divide estate between two real paternal aunts, one consanguine paternal aunt, four uterinal paternal uncles, two uterinal paternal aunts, two real maternal uncles and three real maternal aunts.
Being in the fourth gender they are all eligible. After checking their group and code numbers from Table 2, it is seen that real paternal aunt is in group 19, consanguine paternal sister 20, uterinal paternal uncle 21 and real maternal uncle and aunt are in group 22. Thus group 19 is the lowest. Method 7 will be used to solve this problem.
Based on Method 7, separately list the paternal and maternal relations. In the paternal relatives 19 is the lowest group comprising of real paternal aunts, so only they are entitled to the 2/3 share of the paternal side. Being two in numbers they will receive 1/3 share each. On the maternal side the uncle and aunt will share the 1/3 as per (Liz zikr misl hiz ul unsyn) i.e. both uncles getting twice the share given to aunts. Converting males into females, there are 4+3=7 aunts.
Each receiving 1/3x1/7=1/21. Uncle will get 2x1/21=2/21 and each aunt will receive 1/21 shares.
Method 8
Only difference from Method 7 is that after determining the eligible group, estate will be distributed according to method 1or method 2.
Example 5
Distribute between maternal granddaughters of two maternal grandsons of real paternal aunt, a paternal granddaughter of a maternal granddaughter, maternal grandsons of two maternal granddaughters, three great great paternal grandsons of uterinal paternal uncle and two sons and three daughters of the great granddaughters of the real maternal aunt.
Being in the fourth gender all the heirs are eligible, but some have priority over others. Table 2 shows that descendants of the real paternal aunt, paternal granddaughter of the maternal granddaughter is in group 36, and covered under siblings 2 of the real paternal aunt. The descendants of the uterinal paternal uncle are listed in siblings 3 of the uterinal paternal uncle with group 39. The female descendants of the real maternal aunt are covered under the siblings 3 of the real maternal aunt in group 40. Out of them all, group 36 is the lowest, so according to Table 3, Method 8 will apply here. The descendants of the real paternal aunt are eligible to receive the 2/3 rd share of the father. Descendants of the uterinal paternal uncle will be excluded. Descendants of the real maternal aunt will be eligible to 1/3 maternal shares. Descendants of the real paternal aunt will get shares according to method 2 (See example 1). Descendants of the real paternal aunt will receive as; maternal granddaughter of maternal grandson 2/3x2/7=4/21, paternal granddaughter of maternal granddaughter 2/3x3/14= 1/7 and maternal grandson of maternal granddaughter 2/3x3/28=1/14. Maternal side shares will be distributed according to Liz zikr misl hiz ul unsyn. Converting males into females there are 7 daughters so a daughter gets 1/7 and son 2/7. The remaining estate is distributed as 1/3x1/7=1/21 and 1/3x2/7=2/21.
Simultaneous Death (Ma’nasikha)
Dictionary meaning of ‘ma’nasikha’ is to revoke or compensate. This terminology is basically used to describe the procedure of distributing shares of an heir received from progenitor after his/her demise, between his/her bonafide heirs. It is possible for an heir to not only inherit the estate of the progenitor but also one of the other heirs due to his/her death. The jurists have therefore formulated an easy procedure for the simultaneous distribution of this kind of inheritance. General principle of Mirath is that the claimant of inheritance must be alive at the time of death of the progenitor. Hence, if two mutual heirs die simultaneously, then they cannot inherit from each other.
- Hanbali, Shafii 2and Maliki jurists profess that if sequence of death of two mutual heirs is not ascertained, then it is assumed to be simultaneous. They cannot inherit from each other; this is based on practice of Hazrat Abu Bakr and Hazrat Umar Al-Khttab (RA).
- Shafiis believe that if sequence of death of two mutual heirs cannot be ascertain, then the inheritance is suspended until it is ascertained or there is mutual agreement amongst the heirs on who died first.
- Hanafis think that even if sequence cannot be ascertained; they can still inherit from each other. This is based on view of Hazrat Ali (RA) and Hazrat Abdullah bin Masood (RA).
- If there is simultaneous death of mutual heirs and sequence is known, then this situation is called Manasikha. Inheritance is divided number of times i.e. firstly between immediate kin and then their heirs.
Timely distribution of estate of a deceased can obviate the hassle of ‘ma’nasikha’. Like the other important religious responsibilities being ignored these days, timely transfer of inheritance is generally delayed. Deaths occurring in the family later compel distribution of estates at multiple tiers ranging between many generations. As a result of such inordinate delays things can become complicated. In the reckoning of this author, if total worth of an estate is known, then it is advisable to adopt the routine practise laid down in the Sharia rather then taking recourse to ‘Manasikha’. This will not only be easy but can lend itself to a simple counter check. Beside the progenitor, estate of those expiring later can also be distributed equitably. However in this book working out inheritance with manasikha has been made easy, for those proficient in working with arithmetical fractions. It is, however, advisable to follow the original methodology. Original method involves listing the heirs of each dead person and their shares against each. Once the estate of the progenitor has been asertained; divide it between the eligible heirs. There after distribute estate of the remaining dead amongst their heirs including that received from others. Putting a circle against the name of every dead person, keep on adding his/her receivable shares. To simplify calculations personal assets of the dead should be included here. In order to counter check the calculations, add the personal estates of each dead with the estate of the progenitor, If the sum of the share of all heirs is equal to this figure, then the solution is correct otherwise it has to be re done. To elucidate the working of the both the methods, let’s solve an example.
Example
On her death, Salima left behind a husband Zaid, a daughter Karima and her mother Azima. Before the estate could be divided, Zaid also expired leaving behind his father Omar and mother Rahima. Subsequently Karima also died with two sons Khalid, Abdullah and daughter Raqia left as her heirs. Estate was still to divided that Azima also left for the eternal abode leaving behind her second husband Abdul Rehman ( Salima’s father had died earlier), two sons Abdul Rahim and Abdul Karim and her brother Abdul Rashid. Divide the estate of Salima between the living heirs.
Brother of Azima being the maternal uncle of Salima is a distantly kindred relative thus ineligible along with her step father. After dividing Salima’s estate between her husband Zaid( 6 shares), Daughter Karima (12shares) and mother Azima (4 shares), two shares are left. Since no residuary is alive so these will be returned to the blood related (agnate) primary heirs. To solve the problem, first find out the sum of shares of the agnatic heirs (A), which is 16. Share of the casual primary heirs (C) is 6. Subtracting it from the total shares 24 we get 24-6=18 or S. Multiply A with 18 and C with 16 and the total shares (24) with 16. Resultantly out of the total 384 shares, Zaid will receive 96, Karima 216 and Azima 72 shares. Now out of 24 shares of Zaid, His mother Rahima receives 4, daughter Karima 12 and father Omar 4 shares. Left over 4 shares will also go to Omar as a residuary making his shares 4+4=8.
Estate of Karima after her death is also considered as 24. Azima is her maternal grandmother, Rahima her paternal grandmother and Omar is her paternal grandfather. Her children include two sons Abdullah and Khalid and daughter Raqia. Azima and Rahima in the absence of Karima’s parents and being from the same generation will receive equal shares. Omar being the husband of Rahima, without any linkage with Karima is also eligible to 2 out of the four shares. So Omar will receive a total of 4 shares. Estate between the children will be divided in accordance with ‘Liz zikr misl hiz ul unsyn’. Converting all to daughters makes it five. So after multiplying 24 with 5 we get 120. Now Raqia will receive 16, Khalid and Abdullah 32 each, Omar 20, Rahima and Azima will get 10 shares each.
Azima on her death left behind her husband Abdul Rahman, a brother Abdul Rashid and two sons Abdul Karim and Abdul Raheem. Out of 24 shares of her estate, her husband will receive 6 shares, remaining 18 will be divided between the sons, each getting nine shares.
Total worth of the divisible estate of Salima is Rs. 384000. Zaid who is entitled to 96 out of 384 shares will get Rs.96000 (Unity Method), Karima receives Rs.216000 and Azima gets Rs.72000. Out of Zaid’s share (Rs.96000) after his death, Karima will get Rs. 48000, azima Rs.16000 and Omar Rs.32000. Karima had received Rs. 216000 from Salima and Rs. 48000 from her father Zaid making a total of Rs. 264000. According to unity method Khalid and Abdullah will receive Rs.70400 each, Raqia will get Rs.35200. Besides them Rahima and Azima as grandmothers will receive Rs.22000 and the grandfather Omar will get Rs.44000. Out of Zaid’s estate Omar gets Rs.32000 and Rahima Rs.16000 making their total receivables as Rs. 76000 and Rs.38000 respectively. Azima receives Rs. 72000 from Salima and Rs.22000 from Karima making it Rs.96000.Her husband receives Rs.23500 and sons Rs.35250 each. Adding it all makes 480000 which corroborate the answer as being correct.
Let’s solve it in a different way, supposing that the worth/value of estate is unknown and complete shares have to be determined (no fractions). Find out the shares of all the dead heirs receivable from all others including the progenitor. Make a separate row for each dead heir as shown below (Table A):-
Table A
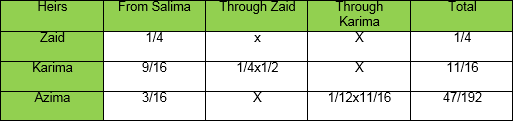
Shares of the live heirs in the estate of dead heirs
Make a separate account of the shares of all living heirs received from the dead heirs including the progenitor. Sum of shares received by a living heir from the dead heirs will be his/her share in the estate of the progenitor e.g. Omar got 1/3 from Zaid and Zaid received ¼ from Salima, so Omar gets 1/3x1/4=1/2 from Salima’s estate through Zaid .Multiply the shares received from a dead heir with the share received by him/her from the progenitor and write it in the columns to determine individual shares.
Table B
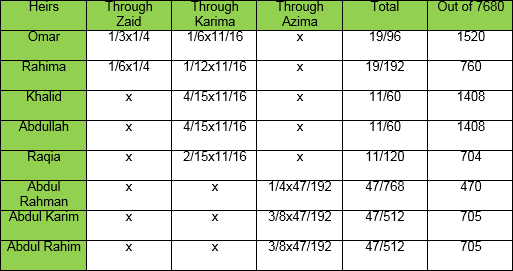
Account of personal Estate of the Dead Heir.
If a dead heir also possessed personal assets, then these have also to be accounted for. In the above example, shares of the dead heir received from Salima’s estate have to be added to their personal assets as shown in the Table below. Zaid received Rs.96000 from Salima’s estate. He also had personal assets worth Rs.100000 raising his estate to 196000. Now Karima instead of receiving Rs.48000 will get Rs.98000. Personal assets of the entire dead heirs have to be similarly added to the shares received by the living heirs from the progenitor.
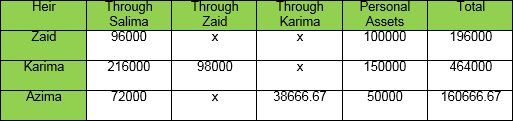
Shares of the Live Heirs
The table below shows shares of live heirs received from the total estate of a dead heir. Calculations have been done according to the unitary method. In accordance with Table 6, Omar receives 19/96 shares from Zaid’s estate. Value of Zaid’s estate is Rs.196000. One third of this given to him is Rs. 65333.33. Karima is receiving 1/6th of Omar’s estate. This share plus her own assets come to Rs.464000. One sixth of her estate is Rs.77333.33. Omar does not get any share from Azima. He only got Rs.142666.67.
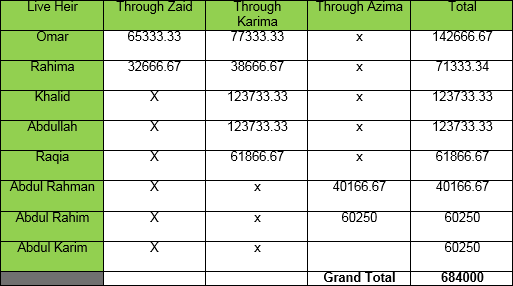
Sum of estate of dead heirs and progenitor is:- Salima: 384000 Zaid : 100000 Karima: 150000 Azima: 50000 Total 684000 Since both totals are tallying so the solution is correct.
Exercise 9
Question 1
Value of estate is Rs.40000. Heirs are husband, Daughter, two paternal granddaughters and a real brother.
Question 2Estate valued at Rs.120000. Heirs Paternal grandfather, three consanguine brothers, one real sister and two uterinal brothers.
Question 3Estate value is Rs.112000. Heirs are a maternal grandmother, paternal grandmother of the father, mother and two consanguine brothers.
Question 4Estate value: Rs.24000. Heirs: Two real sisters, mother, One real paternal uncle, two paternal nephews and one consanguine sister.
Question 5Total estate is valued at Rs.24000.Heirs are three daughters, mother and wife.
Question 6Estate worth: Rs.54000. Heirs are two paternal granddaughters of the maternal granddaughter, one maternal granddaughter of the paternal granddaughter, two maternal grandsons of the paternal grandson, three maternal grandsons of maternal grandson and two paternal grandsons of paternal granddaughter.
Question 7Estate is worth Rs.30000. Heirs are two real maternal nephews, two real maternal nieces and three uterinal maternal nieces.
Question 8- What is the importance of figure 24 in division of inheritance?
- Total estate: 900 Kanals. Heirs: Two paternal granddaughters and three paternal granddaughters of the real sister and two maternal grandsons of the consanguine sister.
Estate: Rs.40000.Heirs: Maternal grandfather of paternal grandfather, Maternal grandfather of paternal grandfather, paternal grandfather of maternal grandfather, maternal grandmother of maternal grandfather and paternal grandfather of maternal grandmother.
Question 10Estate: Rs.18000. Heirs: three paternal granddaughters of the real brother and two maternal granddaughters of the real brother.
Question 11Estate: Rs.90000. Heirs: Two consanguine paternal aunts, one uterinal paternal aunt, three consanguine maternal aunts and one uterinal maternal aunt.
Question 12Estate: Rs.850000. Heirs: Three consanguine paternal cousin brothers, two uterinal paternal (father’s sister) cousin sisters, two uterinal maternal (mother’s brother) cousin brothers, two uterinal maternal (mother’s sister) cousin brothers and an uterinal maternal (mother’s sister) cousin sister.
Question 13Divide estate between three great great paternal granddaughters of the real paternal aunt, two great great paternal grandsons of uterinal paternal aunt, three maternal grandsons of uterinal maternal aunt and two maternal granddaughters, two great great paternal grandson and four great great paternal granddaughters of consanguine maternal uncle.
Question 14Divide estate between two real and three consanguine sisters.
Question 15Naeem on his demise left behind his wife Samina two daughters Shakila and Sajida , mother Naheed and father Abdul Majid. Before the estate could be divided Abdul Majid also expired leaving behind his wife Naheed, three daughters Karima, Salima and Naeema and son Abdul Akbar. Before both the estates could be divided, Naheed also died. A little while later, Abdul Akbar also breadth his last, leaving behind Jamila, his wife and son Shahid. How will the estate of Naeem be divided in the living heirs?
Question 16Find out the shares of wife, three daughters and a consanguine sister in the estate left behind by Junid?
Question 17Divide Salim’s estate amongst his two feminine ancestors, a real sister, a real paternal nephew and a real paternal cousin sister.
Question 18Work out the shares of three wives, two uterinal brothers, three real sisters and two consanguine sisters in the estate left behind by Arshad?
Question 19Find out shares of Zaid’s two real sisters, three consanguine and four uterinal sisters?
Question 20Divide estate amongst three real paternal nieces, one real sister’s daughter and a uterinal sister’s son?
Question 21How will the estate of Shahid be divided in his two maternal grandsons and three maternal granddaughters of his paternal granddaughter, two paternal grandsons of his maternal grandson and five paternal granddaughters of his maternal granddaughter?
Question 22Distribute estate of Sajid in two daughters of his sister, mother, paternal and maternal grandmothers?
Question 23Divide estate among father of paternal grandmother, father and mother of maternal grandfather and father of maternal grandmother?
Question 24Allot shares to a real sister, one consanguine and one uterinal sisters?
Question 25Distribute estate among daughters of real brother, two sons and three daughters of the real sister?
Question 26Divide estate in two real paternal aunts, one consanguine paternal aunt, four uterinal paternal uncles, two uterinal paternal aunts, two real maternal uncles and three real maternal aunts?
Question 27Allot estate to two grandsons of maternal grandsons, one paternal grandson of maternal granddaughter?
Question 28Divide estate amongst husband, three consanguine sisters, one real sister, mother, paternal great grandfather and mother of paternal grandfather?
Question 29Solve questions 23and 35 in accordance with the professed by Imam Abu Yousaf.
Chapter 10 – Equations
Definition
An equation says that two things are the same, using mathematical symbols. Equal variables are also represented by an equation. Variables have no constant value and are represented by letters.
An equal sign (=) is used
Example: 7+2 = 10-1
What is an Equation
An equation says that two things are equal. It will have an equals sign "=" like this:
x + 2 = 6
That equation says: what is on the left (x + 2) is equal to what is on the right (6)
So an equation is like a statement "this equals that"
Parts of an Equation
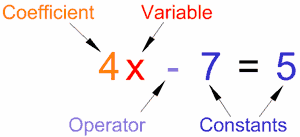
A Variable is a symbol for a number we don't know yet. It is usually a letter like x or y.
A number on its own is called a Constant.
A Coefficient is a number used to multiply a variable (4x means 4 times x, so 4 is a coefficient)
An Operator is a symbol (such as +, ×, etc) that represents an operation (ie you want to do something with the values).
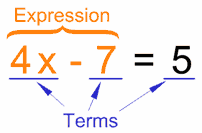
A Term is either a single number or a variable, or numbers and variables multiplied together.
An Expression is a group of terms (the terms are separated by + or - signs).
Addition of Algebraic Variables
In addition of variables with the same sign it is not changed and their coefficients will be simply added.
+ 2x + 7x + x = +10x or -x + (-3x) + (-2x) = - 6x
In case of different signs variables with + sign will be added separately and those with the minus sign separately. Their sum will be subtracted from each other and the dominant sig will be retained e.g.
+2x - 3x – 5x + x – 4x + 6x = + 9x – 12x = - 3x
In addition of variables the sign is not changed e.g. +2x + (-x) = 2x – x. In subtraction however their signs are reversed e.g. 4x – (-3x) = 4x + 3x and 7x – (+2x) = 7x – 2x
In the multiplication of variables if signs are same then the product will have a + sign but in case of dissimilar signs product will carry a - sign e.g. (+2x) x (+3y) = + 6xy and (-4y) x ( -3c) = + 12cy but,
(+2a) x (-3b) = - 6ab
(-2a) x (+4b) = - 8ab
Characteristics of Equations
- Addition, subtraction, multiplication or division of two sides of an equation will make no difference.
- Shifting of a constant or a variable to either side of an equation will result in change of its sign. A plus will change to minus and multiplication to division.
Example
12 + 3b = 6c – 2d
Subtraction of 3b from both sides,
12 + 3b – 3b = 6c – 2d – 3b
6c – 2d -3b = 12
Notice that 3b was added on the right side but subtracted on left. So it made no difference to the equation. It is therefore said that the second characteristic is a result of the first characteristics.
Simultaneous Solution of Two or more Equations
This is a very useful method. Let’s take following equations:-
a + 2b = 8
3a – 5b = 2
First step is to remove the variables. In the first equation if both sides are multiplied with 3 and second equation is subtracted from the first then,
3a + 6b = 24
3a – 5b = 2
__________
11b =22
b = 2
Example
Some people are two sitting on two cots. If a person moves to another cot then the number of people on both cots will become equal. If a person shifts from the first to second cot number of persons on it will be doubled. How many persons are sitting on each cot?
Suppose ‘a’ persons are sitting on the first cot and ‘b’ persons on the other one. With moving of a person from one another cot the number becomes equal on both the cots. So:-
a – 1 = b + 1
Adding 1 to a and subtracting it from b doubles the number
a + 1 = 2 (b-1)
These are two equations now. Two values have emerged by working on equations in both the boxes,
a = b + 2
a = 2b – 3
Solving them together,
a = b + 2
a = 5 +2 = 7
Quadratic Equations
This is what a "Standard" Quadratic Equation looks like:

- The letters a, b and c are coefficients (you know those values). They can have any value, except that a cannot be 0.
- The letter "x" is the variable or unknown (you don't know it yet)
Here is an example of one:
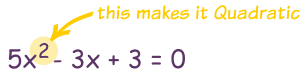
Quadratic Formula
Equations with variables of exponential power of up to 2 is called a quadratic equation e.g. ax2 + bx +c = 0. Maximum power of the exponent is 2. This is a very useful equation for finding unknown values. Taking a, b and c as constants and x as a variable the quadratic equation is
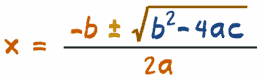
About The Quadratic Formula
Plus/Minus
First of all what is that plus/minus thing that looks like ±?
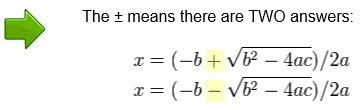
Discriminant
Do you see b2 - 4ac in the formula above? It is called the Discriminant, because it can "discriminate" between the possible types of answer:
- when b2 - 4ac is positive, you get two real solutions
- when it is zero you get just ONE real solution (both answers are the same)
- when it is negative you get two Complex solutions
Example 1
Solve 5x² + 6x + 1 = 0
Coefficients are: a = 5, b = 6, c = 1
Quadratic Formula: x = [ -b ± √(b2-4ac) ] / 2a
Put in a, b and c: x = [ -6 ± √(62-4×5×1) ] / (2×5)
Solve: x = [ -6 ± √(36-20) ]/10 x = [ -6 ± √(16) ]/10 x = ( -6 ± 4 )/10 x = -0.2 or -1
Example 2
Solve the following quadratic equation:-
2y2 – 100y +1200 = 0
Here a= 2, b= - 100 and c = 1200
So applying the quadratic formula
x=(-b±√(b^2-4ac))/2a
X = - (-100) ± √ (-100)2- 4 x 2 x 1200 / 2x2
X = 20
Similarly
X = - (-100) ± √ (-100)2 – 4 x 2 1200 /2 x 2
= 30
Exercise 10
Question 1
Arshad has secured 5 marks less than Anwar. Total of their secured marks is 119. How many marks has each of them secured?
Question 2After division of a number with 7 and addition of 3 to the quotient become 24. What is the number?
Question 3A rectangular piece of land has a circumference of 100 meters and its area is 600 square meters. Find the length and breadth of the land?
Question 4Find out two numbers whose sum is 8 and product of their multiplication comes 7?
Question 5Sum of a two digit number is 13. When the digits are swapped their sum is increased by 45. Find the number?
Question 6Present age of a father is thrice the age of his son. After five years it will reduce to two and half times. What are their present ages?
Question 7A person out his money for charity gave one third to a school, fifth to a hospital and one sixth to an orphanage. He donated the remaining balance of Rs.12150 to a mosque. How much did he spend?
Question 8Find the number the sum of who’s third, fourth and fifth is 94?
Question 9An aero plane was observed by two opposite observation posts. Distance between the posts is 5 kilometers. Angles of observation are 30 and 40 degrees respectively. Find the altitude of the aircraft?
Question 10To hire a bus, if all students pay Rs.5 per head there is a surplus of Rs.12. Payment of Rs.4.5 per head leaves a deficiency of Rs.13. Find the number of students and fare of the bus?
Chapter 11 – Geometry & Trigonometry
Geometry was invented for the measurement of land. Plane geometry is about flat shapes like lines, circles and triangles. The subject encompasses the explanation of points, lines, angles, planes, and shapes that exist in the universe and those that can be drawn on a piece of paper. Where as solid geometry deals with three dimensional objects like cubes prisms and pyramids. Explanations, principles and rules, concepts and their inter connectivity are dealt in the subject.
Basically two cardinal principles regulate the subject. The fixed principles are those which are accepted without reasoning. Those where discussion on logical grounds is permitted are called the principles.
Definitions/ Explanations
Point
A point is an expression or reference indicator of a location or a place in the universe which otherwise can not be described. It has no dimensions like length, width or thickness but possesses an entity. A dot on a paper is the indicator of a point which is though not visible but has dimensions far beyond a dot.
Line
A line is a straight one-dimensional figure having no thickness and extending infinitely in both directions. Or. A line represents the union of two points. It can have an indefinite length but possesses no thickness.
Angles
An angle is the rotation required to superimpose one of two intersecting lines on the other.
Right Angle
A right angle is an internal angle which is equal to 90°
This is a right angle
Measurement of Angles
We often measure degrees using a protractor. The normal protractor measures 0° to 180°.
Acute Angles
An Acute Angle is less than 90°.
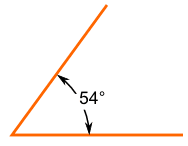
This is an acute angle
Right Angle
A right angle is an internal angle which is equal to 90°.

This is a right angle
Obtuse Angle
An Obtuse Angle is more than 90° but less than 180°
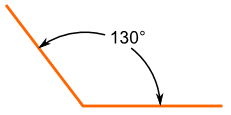
This is an obtuse angle
Supplementary Angles
Two Angles are Supplementary if they add up to 180 degrees.
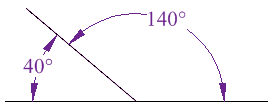
Complimentary Angles
Two Angles are Complementary if they add up to 90 degrees (a Right Angle).
Triangles
A triangle has three sides and three angles, which always add up to 180°.
Type of Triangles
- Acute Triangle. All angles are less than 90°
- Right Triangle. Has a right angle (90°).
- Obtuse Triangle. Has an angle more than 90°
Equilateral Triangle
Three equal sides. Three equal angles, always 60°.
Isosceles Triangle
Two equal sides. Two equal angles.
Scalene Triangle
No equal sides. No equal angles.
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves. The field evolved during the third century BC as a branch of geometry used extensively for astronomical studies. It is also the foundation of the practical art of surveying. Knowledge of trigonometric functions and methods reached Europe from the works of Arabic astronomers such as Al Battani, Al Barooni, Nasir al-Din al-Tusi and Muhammad bin Musa Al Khawrzami.
If one angle of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are complementary angles. The shape of a triangle is completely determined, except for similarity, by the angles. Once the angles are known, the ratios of the sides are determined, regardless of the overall size of the triangle. If the length of one of the sides is known, the other two are determined.
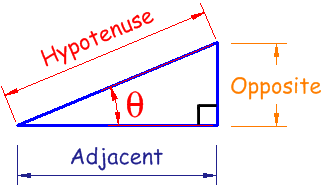
These ratios are given by the following trigonometric functions of the known angle A, where a, b and c refer to the lengths of the sides.
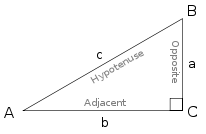
Hypotenuse2 = adjacent2 + opposite2
AB2 = AC2 + BC2
Sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.
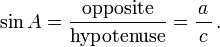
Cosine function (cos), defined as the ratio of the adjacent leg to the hypotenuse.
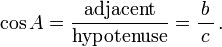
Tangent function (tan), defined as the ratio of the opposite leg to the adjacent leg.
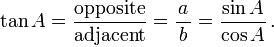
Pythagorean Theorem
The Pythagorean Theorem or Pythagoras' theorem is a relation among the three sides of a right triangle (right-angled triangle). In terms of areas, it states:
In any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).
The theorem can be written as an equation relating the lengths of the sides a, b and c, often called the Pythagorean equation.
a2 + b2 = c2
Where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides. The sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse (c).
Example
A stair is resting 8 meter high against a wall. Its base is 6 meters away from the wall. Find length of the stair?
This can be solved with the help of Pythagorean Theorem. Here we know the lengths of the adjacent and opposite. Putting these values in the formula will give us length of the stair.

a2 + b2 = c2
c2 = 36 + 64 = 100
c = 10
Solutions of Right Angle Triangle
As pointed out in the introduction, if c denotes the length of the hypotenuse and a and b denotes the lengths of the other two sides, the Pythagorean Theorem can be expressed as the Pythagorean equation:
a2 + b2 = c2
If the length of both a and b is known, then c can be calculated as follows:
c = √ (a2 + b2)
If the length of hypotenuse c and one leg (a or b) are known, then the length of the other leg can be calculated with the following equations:
a = √ (c2 - b2)
OR
b = √ (c2 - a2)
The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the legs, but less than the sum of them.
Angles of Inclination/Elevation and Declination/Depression
Angles of elevation or inclination are angles above the horizontal, like looking up from ground level toward the top of a flagpole. Angles of depression or declination are angles below the horizontal, like looking down from your window to the base of the building in the next lot. Whenever you have one of these angles, you should immediately start picturing how a right triangle will fit into the description.
The horizontal line across the top is the line from which the angle of depression is measured.
- Measure the height and distance of a building in the enemy territory without physically going to it, for engagement.
- To measure the width of a water body without swimming across it.
- Determination of afternoon prayer (asar) timings.
- Location of stars and other planetary bodies.
Sine, Cosine and Tangent
The three main functions in trigonometry are Sine, Cosine and Tangent.
They are often shortened to sin, cos and tan.
To calculate them:
Divide the length of one side by another side. but you must know which sides!
For a triangle with an angle θ, the functions are calculated this way:

Sine Function: sin(θ) = Opposite / Hypotenuse
Cosine Function: cos(θ) = Adjacent / Hypotenuse
Tangent Function: tan(θ) = Opposite / Adjacent
sin B = AC / BC cos B = AB / BC tan B = AC / AB sin C = AB / BC cos C = AC / BC tan C = AB / Ac
Example
A tower is 100 feet away from the point of observation. Elevation angle to its top is 60 degrees. Find height of the tower?
This is the first form where an angle and a side of are known. So,
Height of tower = AC Angle of Inclination = 60 degrees Distance from Observer = AB = 100 Tan 60 = AC / AB 1.73205 = AC / 100 AC = 1.73205 x 100 = 173. 205 Height of Tower = 173. 205 feet.
Second Form
An angle and hypotenuse are known.
Example
Angle A is 30 degrees and side AC is 5 cms
BC / AC = BC / 5 = sin 30 = 0.5 BC = 5 x 0.5 = 2.5 AB / AC = AB / 5 = cos 30 = 0.866 AB = 5 x 0.866 = 4.33 In a right angle triangle sum of two angles is 90. Since one angle is 30 therefore 90 – 30 = 60 So the other angle is 60 degrees.
Third Form
When two sides of a right angle triangle are known then hypotenuse can be found with application of Pythagorean Theorem.
If the length of both a and b is known, then c can be calculated as follows:
c = √ (a2 + b2)
If the length of hypotenuse c and one leg (a or b) are known, then the length of the other leg can be calculated with the following equations:
a = √ (c2 - b2)
b = √ (c2 - a2)
Sum of the two angles is 90, so if one is known the other can be easily found.
Example
To engage a bunker in the hostile territory its distance and height are required to be found. Observations from point A and B resulted in 45 degrees and 40 degrees angles of inclination to C (bunker). Distance between the observation point A and B is 100 feet. Find the distance and height of the bunker?
SC/AC = tan 40 = 0.8391 SC/BC = tan 45 = 1.0 SC = 0.8391 x AC = SC = 1.0 x BC 0.8391 x AC = 1.0 x BC 0.8391 x (BC + 100) = BC 0.8391BC + 83.91 = BC BC – (1.0 - 0.8391) = 83.91 BC - 0.8391BC = 83.91 0.1609 BC = 83.91 BC = 521.5 SC = 521.5 x 1.0 = 521.5 So the height of the bunker is 521.5 feet and the distance to its base from observation point B is 521.5 feet.
Example
Radius of the earth is approximately 3986 miles. What will be rotational speed of earth on a place at the equator? What will be the rotational speed of earth at Multan which is located at 30degrees latitude?
The first thing to determine is the circumference of the latitude.
Circumference = 2 × π × Radius Radius of the earth at the equator is 3986 miles. So Circumference = 2 x π x 3986 = 25046 miles Since the earth completes a circle in 24 hours, so speed of earth at a place on the equator is 1043 miles per hour. At 30 degrees latitude line AB is parallel to the equator, which represents the radius of the latitude. Whereas at the equator the diameter is equal to the radius of the earth, it is not so at other latitudes. These are smaller circles. In the triangle ABM, angle MAB is 30 degrees and the radius (line AM) is 3986 miles. So AM x cos 30 = AM x 0.866 = 3986 x 0.866 = 3452miles Circumference of the circle at 30 degrees = 2x π x 3452 = 21690 miles Rotational speed per hour = 21690 ÷ 24 = 903.75 So the rotational speed of earth at a place at 30 degree latitude is 903.75 miles per hour.
An Important Conclusion
Longitudes have 360 degrees, so a difference of 4 minutes occurs between two degrees. As seen in the previous example rotational speed of a place located at the equator is 1043 miles per hour, which means that a difference of one hour occurs after every 1043 miles. To determine the distance per minute solve 1043 ÷ 6 = 17. 38 miles.
At 30 degree latitude = 17.38 x cos 30 = 17.38 x 0.866 = 15.05 miles
At 60 degree latitude = 17.38 x cos 60 = 17.38 x 0.5 = 8.69 miles
Finding Angles with Trigonometric Functions
If a function of a triangle is known then it is to find its angle by inversing the result.
Example
Tan C = 1.0. Find angle C?
Write 1.0 on a calculator. After pressing the inverse button, press tan button. Answer displayed is 45, which is angle C.
Example
A 60 cm pole is fixed perpendicular to the ground. It subtended shadow is 30 cm. What is the angle of the sun with the pole?
Shadows of the pole and the sun are making a right angle triangle ABC. Angle NCS have to be found. We know that angle NCS is equal to angle CAB. So both angles have the value being . In the above triangle tan ACB is 26.58. Inversing it on a calculator will give us the angle which is equal to angle the sun is making with the pole.
Tan ABC = AB/ BC = 30/60 = 0.5
< ABC = tan-1 (0.5) = 26.56
Exercise 11
Question 1
Find supplementary and complimentary angles of 420 ?
Question 2In a right angle triangle one side is 45 and the other is 35. Find its hypotenuse and all its angles?
Question 3In the figure below find the other sides and angles, with help of the given information.
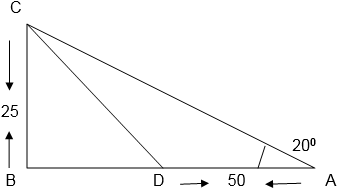
Question 4
How will you find the height of a hill without climbing it?
Question 5A hostile aircraft is located at point C. Its angle of inclination from point A is 350 and from point B it is 450. Point B is located to the east at a distance of 3000 m. The aircraft is flying from point B towards the west. How far the plane from point B and what is is its altitude?
Question 6An object one meter high cast a shadow of 31 cm on a plain ground near the sun set. What was its angle of inclination with the sun?
Question 7At a place direction of Qibla makes an angle of 1070 with the north. Find length of a line drawn from the north to link it to a point where from a one meter line drawn in westerly direction joins it, to indicate direction of the Qibla?
Chapter 12 – Area and Volume
This is an important part of Geometry. Finding the area and volume of various shapes is needed during the demarcation of land for distributions among the successors in transfer of inheritance. A piece of land is divided into squares and triangles and then measured accordingly with the help of formulas. It is important for the scholars to be proficient lest they are hoodwinked by crooks. It also important to fear Almighty Allah and ensure that no one is denied their rights because of negligence or lack of requisite knowledge.
Area
Area is the amount of space inside the boundary of a flat object (such as a square or circle.
Area of Square
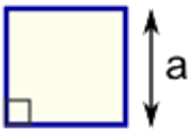
Area = a2
a = length of side
Area of Circle

Area = πr2
Circumference = 2πr
r = radius
Area of a Triangle
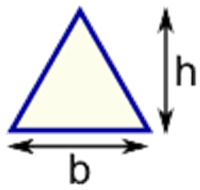
Area = ½b × h
b = base
h = vertical height
Example
Sides of a triangle are 15 feet, 10 feet and 9 feet. Find the area? Area of a triangle =√ (s (s-c) (s-b) (s-a)) S = a+b+c /2 = 9+15+10 / 2 = 17 Area = √ 17 (9-17) (10-17) (15-17) = √ 1904 = 43.63 square feet
Area of a Rectangle
The formula is: Area = w × h w =width h = height The breadth is 5, and the height is 3, so we know w = 5 and h = 3. So: Area = 5 × 3 = 15
Besides the above formula area of a rectangle can be found by splitting it into triangles as shown in this figure.
Volume
Cuboids
A cuboid is a 3 dimensional shape. So to work out the volume we need to know 3 measurements.
Look at this shape.
There are 3 different measurements:
Height, Width, Length
The volume is found using the formula:
Volume = Height × Width × Length
This can be shortened to:
V = h × w × l
Volume of a Cylinder

Just multiply the area of the circle by the height of the cylinder:
- Area of the circle: π × r2
- Height: h
- Volume = Area × Height = π × r2 × h
- Π = 3.14
Example 1
A well with a radius of 6 feet has 9 feet of standing water in it. The bucket used to draw water has length of 2 feet and a radius of 6 inches. Find the volume of water in the well. Also work out the number of buckets it contains?
Radius of well = 6 feet
Depth of water = 9 feet
Volume of water = π x 6 x 6 x 9 = 1017.873 cubic feet
Radius of bucket = 6 inches = 0.5 feet
Length of bucket = 2 feet
Volume of bucket = π x .5 x .5 x 2 = 1.0798 cubic feet
Number of buckets = 1017.873 ÷ 1.0798 = Approx 648
Example 2
Measure a plot whose dimensions are given in feet?
First divide the plot into triangles as shown in the diagram below. Number each triangle and measure its sides and apply the formula:
Area = =√ s (s-c) (s-b) (s-a)
There are 10 triangles. Add up area of each one of them to find area of the land.
1. 12+30+32 / 2 = 37 , √ 37(12-37)(30-37)(32-37) = 179.93 2. 32+14+36 / 2 = 41 , √ 41(32-41)(14-41)(36-41) = 223.2 3. 32+14+34 / 2 = 42 , √ 42(32-42)(14-42)(34-42) = 237.59 4. 32+14+36 / 2 = 42 , √ 42(32-42)(14-42)(34-42) = 237.59 5. 41+36+15 / 2 = 46 , √ 46(41-46)(36-46)(15-46) = 267.02 6. 41+14+41 / 2 = 46 , √ 46(41-46)(14-46)(41-46) = 257.37 7. 17+37+42 / 2 = 48 , √ 48(17-48)(37-48)(42-48) = 313.38 8. 36+14+42 / 2 = 46 , √ 46(36-46)(14-46)(42-46) = 242.65 9. 44+18+36 / 2 = 49 , √ 49(44-49)(18-49)(36-49) = 314.22 10. 35+17+44 / 2 = 48 , √ 48(35-48)(17-48)(44-48) = 278.16 Total = 2551.21
Example 3
A school wall measuring 20 feet in length, 9 inches thick and 10 feet high has to be constructed. Dimensions of a brick are, thickness 3 inches, length 9 inches and width 4.5 inches. Work out number of bricks needed?
Volume of wall = Height × Width × Length = 20 x 9/12 x 10 = 150 cft
Volume of a brick = Height × Width × Length = 9/12 x 3/12 x 9/2 x 1/12 = 243/3456 cft
Number of bricks = 150 ÷ 243/3456 =2133.33 say 2134 bricks.
Exercise 12
Question 1
Find area of a circle whose radius is 4.5 inches?
Question 2
One side of a rectangle 41 cm and the other side is 54 cm. Find its area?
Question 3
Find area of the rectangle shown below. Dimensions of a, b, c and d are indicated.
Question 4
A well with a radius of 3 feet has 10 feet of standing water. Find volume of water? How many buckets of water does it contain? Dimensions of the bucket are; depth 1.5 feet and its opening is 14 x 14 inches.
Question 5
How many bricks of 4.5 x 9 x 3 inches will be required to construct a room whose walls are 10 feet high, 9 inches thick and total length of walls is 45 feet? If width of the room is 10 feet work out the area of its roof?
Question 6
To preserve books in a library, its bindings on both sides have to be covered with paper. Length of a book is 10 inches, width 5.5 inches and an average thickness of one inch. How much of paper will be required to cover 150 books?
Question 7
A water tank has to be constructed in a school for 400 persons. A person needs 5 litres of water per day. What should be height of the water tank measuring 4 x 5 feet?
1 cubic foot = 28.316847 litres
Chapter 13 - Spherical Trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons (especially triangles) on the sphere and the relationships between the sides and the angles. This is of great importance for calculations in astronomy and earth-surface, orbital and space navigation. This knowledge can be applied to solve many of our religious problems e.g. finding the qibla direction, timings of prayers and determination of distances in jihad. A large part of astronomy is based on the subject.
In the early 9th century, Muhammad ibn Mūsā al-Khwārizmī, a Persian mathematician, was an early pioneer in spherical trigonometry and wrote a treatise on the subject. In the 10th century, another Persian mathematician Abū al-Wafā' al-Būzjānī established the angle addition formulas, e.g., sin (a + b), and discovered the sine formula for spherical trigonometry:
Here, a, b, and c are the angles at the centre of the sphere subtended by the three sides of the triangle, and α, β, and γ are the angles between the sides, where angle α is opposite the side which subtends angle a, etc. In this formula relationships of any two sides and their angles can be used.
Cosine Formula
Given a unit sphere, a "spherical triangle" on the surface of the sphere is defined by the great circles connecting three points’ u, v, and w on the sphere (shown above). If the lengths of these three sides are a (from u to v), b (from u to w), and c (from v to w), and the angle of the corner opposite c is C, then the (first) spherical law of cosines states:
The formula is used to express the relationship of sides with an angle. A thing to remember here is that unlike an ordinary triangle where the sum of all three angles is1800, in a spherical triangle it is not true. Sum of the three angles is more than 1800.
A variation on the law of cosines, the second spherical law of cosines. (also called the cosine rule for angles) states:
Where A and B are the angles of the corners opposite to sides a and b, respectively. It can be obtained from consideration of a spherical triangle dual to the given one. Here relationship of a side with all angles can be expressed.
These laws are used to any one of the six elements. Selection of the corresponding rule is essential e.g. in a spherical triangle we want to find B when C, b and c are known. So when we see all the formulae, it is the Sine Formula which expresses the relationship of these values, sin b/sin B = sin c/ sin C. By putting in the known values those which are unknown can be found e.g. all sides are known and angle C has to be found. Cosine formula I will be used:-
cos C = cos A cos B + sin A sin B cos c
When all angles are known and a side has to be found then a variation of Cosine formula 2 is applied. When angles of A, B, and C are known and value of a has to be found, then
cos A = cos B cosB cos C + sinB sin C cos a
Example
In the spherical triangle shown here, b = 90.8330, c = 66.670 and a = 56.25. Find angle C?
Here Cosine formula 2 applies:-
cos c = cos a cos b + sin a sin b cos C cos90.833 = cos66.67 x cos56.25 + sin66.67 x sin56.25 x cos C cos C = cos90.833 – cos66.67 x cos56.25 = cos90.833 – cos66.67 x cos56.25 ÷ sin66.67 x sin56.25 = cos-1 (cos c – cos a cos b) ÷ sin a sin b = cos-1 ( - o.014538 – 0.39603 x 0.55557 ÷ 0.7634878 = 107.89
So angle is approximately 1080.
Sometimes one angle and two sides are known and the other angle has to be found.In such a situation one way is to find the third side and putting the known values in the equation the second angle is found. The other method is to use the Sine formula.
B = tan-1 (sin C / sin a cot b – cos a x cos C
Both these methods are used to determine the direction of Qibla. Suppose the North Pole is C. Makkah is point A and the place where the Qibla has to be found is B. Line AB is the line joining both these places. The longer this line more is the distance from Makkah. Angle B will indicate the direction of Qibla. Line BC is the line to the North Pole and angle B is the angle of Qibla to the north.
a = 90 – M and sin (90- M) = cos M M being the latitude of the place.
b = 90 – Ma and tan (90 – Ma) = sin Ma Ma being the latitude of Holy Makkah.
cos 90 – M = sin M and c = longitude of Makkah – longitude of place
B = tan-1 (sin c ÷ cos LAT x tan LATM – sin LAT x cos C. In this formula, if the product is in minus then add 180 degrees and both and then subtract from 180 degrees.
Example
Longitude and latitude of Islamabad are 73.05 easting and 33.43 northing. Find Qibla angle for Islamabad? Longitude and latitude of Makkah being 39.45 easting and 21.449998 northing.
Latitude (LAT) = 33:43 =33.716676 Longitude (LONG) = 73:05 = 73.08333 Longitude Makkah = 39:45 = 39.75 (LONGM) Latitude Makkah = 21.4499986 (LATM) C = 39.75 – (- 73.0833) = 33.3333 B = tan-1 (sin 33.3333 / cos 33.7167 x tan 21.45 – sin 33.7167 x cos 33.33 = - 760 Since the product has a minus sign so 180 - 76 = 1040 Direction of Qibla in Islamabad will make an angle of 1040 with the north.
Exercise 13
Question 1
In this figure if value of a is 600, b is 850 and c is 1050. Find the value of C?

Question 2
In the same figure if a is 550, b is 800 and angle C is 920. Find the value of angle B?
Question 3
In question 2, find the value of angle A?
Question 4
A table of longitudes and latitudes is given in the table below. What will be angle of Qibla with the north at every place?
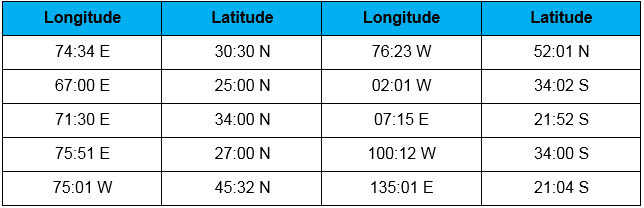
Question 5
Find the aerial distance from Karachi to the places given in the table? Location of Karachi is Longitude 670 E and Latitude is 250 N.
Hint If the given place is in east of Karachi then using figure in question 1 a = 90 – Lat b = 90 – Lat Karachi Angle C = Lat – Lat Karachi If the place is located west of Karachi:- b = 90 – Lat a = 90 – Lat Karachi Angle C = Lat Karachi - Lat
Chapter 14 – Computers
Introduction
Computer is a useful tool which can be employed to solve many of our day to day problems quickly. Every passing day its usage is increasing in all field of life. It can be effectively used in the religious schools. A fairly large number of people are sceptical to become computer literates because of what they have been hearing about its misuse. Learning to use a computer is very easy; however it has no magical powers to find solution to all the problems. It works like a child who cannot think but is a fast worker. If you speak to him in the language that he understands, then he will deliver quickly. Basically it all depends on us; what to tell him; right or wrong things. He will simply do it without understanding its implications.
A computer is a programmable machine designed to automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem. An important class of computer operations on some computing platforms is the accepting of input from human operators and the output of results formatted for human consumption. The interface between the computer and the human operator is known as the user interface.
Conventionally a computer consists of some form of memory, at least one element that carries out arithmetic and logic operations, and a sequencing and control unit that can change the order of operations based on the information that is stored. Peripheral devices allow information to be entered from an external source, and allow the results of operations to be sent out.
A computer's processing unit executes series of instructions that make it read, manipulate and then store data. Conditional instructions change the sequence of instructions as a function of the current state of the machine or its environment.
Basically a computer is a machine that can be programmed to do things with data. Computers can usually: * "input" data from a mouse, keyboard or touch-screen, * "process" the data using a CPU and memory, and * "output" the result onto a screen or save it to disk.
Binary Numbers
A Binary Number is made up of only 0s and 1s. 110 is a binary number (which is equal to 6 in the decimal system we normally use). In the computer world "binary digit" is often shortened to the word "bit"
This is the basic computer language. English letter in binary language is expressed as 0010011.
Terminology
Computer Hardware
Basic components of a computer are called its hardware. These are related to electronic engineering and technology.
Software
These are computer programmes used for its applications and programming.
Hard disc
A disc located inside a computer where all programmes are stored.
Floppy disc
A circular disc which contains limited data. It can shift data from one computer to another.
Computer Programme
It is a set of instructions to control operation of a computer and its components like hard disc, floppy discs and CD Rom etc. A disc control system is called Disc Operating System (DOS).
Programmer
Programmer is a Person writing the programmes.
Computer Language
Language used to impart instructions to a computer by a programmer is called High Level Language. This is then converted to a machine language which is called Low Level Language. The programme which converts the language is called a Compiler.
Windows and Other Operating Systems
These are the inbuilt programmes to run computer programmes. Many variations are available these days. Windows is a popular operating system.
Computers are run with two types of programmes. One a ready made programmes which have to be leant with the help of manuals or its ‘Help’ facility. Other programmes are used by the programmers who have gained expertise in computer languages.
Precautions
Uncontrolled use of computer especially internet can be harmful for children.
Use for Education
A computer can be effectively used for educational purposes. Lessons with audio video effects can be prepared for better assimilation.
Recordings
A computer is a better recording tool. It has a better quality and is cheap.
Calculation of Sadaqah e Fitra
In our part of the world sadqah e fitr is associated with the price of wheat. It is better to work on the price prevalent then. Suppose price of wheat is Rs.9 per kg, so
1.635876 x 9 = 14.722884 say Rs.15
So sadqah e fitr per head is Rs.15.
Ten by Ten Rule (10 x 10)
A pond measuring 10 hands (1.5 feet/hand) in length and 10 hands has clean water. This 15 x 15 feet is covered under the doctrine of ten by ten. This rule states that despite some filth lying on one of its sides; it is permissible to perform ablution with the water. A rectangular pond with an area of more than 225 sq feet will fall into the category of ten by ten. Sharia has only permitted calculation of the area. Volume is not included because of the uncertainty of the depth of water.
Example
A pond measures 20 feet in length. What should be its width to qualify for ten by ten doctrine?

20 x W = 225 W = 225 ÷ 20 = 11.25 feet Out of the total permissible area of 225 sq feet one side is 20 feet. The other side as calculated above should be 11.25 feet.
Example
Calculation of the figure below show that in a circular pond the diameter should be 8.463 feet or more to qualify for Ten by Ten Rule.

Area = πr2 r = radius Area = πr2 = 225 Π = 3.14159 = √ 225 / 3.14 = 8.463 feet
Answers – Exercises
Exercise 1
1. (3, 22.4) 2. (416.50, 8.50) 3. (227750) 4. (Rs.13225.25) 5. (Total Expenditure isRs.2865500)
Exercise 2
1. 59/72 2. Rs288000 3. 5/72 4. 345/894 5. 15/28 6. 5 litres 7. 35cm 8. Rs 900
Exercise 3
1.Rs28800 2. 9Litres 3. Rs11250 4. 9 days 5. 48 miles 6. 2809 poles and cloth 1373962.5 sq feet 7. Rs177777, 474074, 237037, 2370238 8. Half hour
Exercise 4
1.16.67% 2. Rs.137500 3. Rs24075 4. Rs857.38 5. Akram 50%, Aslam 30% and Zubair 20% 6. Rs775 7. 19.65% profit 8. 90% profit 9. Rs.15000 profit 10. Rs15000 profit 11. Rs90000 loss 12. Rs.4000 13 52.323% profit.
Exercise 5
1. 3:2::4:4 2. 16/3 3. Rs2700 4. Rs1500 6. (300, 600) 7. (14000, 10000) 8. (400, 300) 9. (30000, 20000, 15000) 10. (30600, 20400) 11. (12600, 8400) 12. 31.990
Exercise 6
13. Rs184.21 14. – 65 15. Rs.170 16. - 44 17. Old school : 45 , new school: 37.
Exercise 7
1.316.228 2. 258.386 3. 0.008 4. Power 10 5. Log (1.7+1.4+1.5) 6. ¼ log 16 7. 3.80662 8. 45
Exercise 8
1.Satureday 19th Rabi ul Awl 1378 2. 16th March 624 3. 12th Hira 1337 4. 26th Ahad 2 5. 5th October 6. 20th Jamdi ul Akhar 748
Exercise 9
1. Husband 3, daughter 6, paternal granddaughter 1, real brother 1 2. Paternal grandfather will receive all shares excluding others. 3. Mother 1, consanguine brother 2 with rest excluded. 4. Mother 2, real sisters’ 4 and real paternal nephew 1. 5. Mother 21, wife 15 and each daughter 28. 6. Maternal grandson of paternal grandson ½ each while rest are excluded. 7. Each real maternal nephew 2, each real maternal niece one and every uterinal nephew one. 8. Paternal grandsons of real sister 2 and each paternal granddaughter if real sister one. 9. Maternal grandfather of paternal grandfather 18, paternal grandfather of maternal grandfather 4, maternal grandmother of maternal grandfather 2 and paternal grandfather of maternal grandmother 3. 15. Samina 15,Shakila 40, Sajida 40, Karima 8, Salima 8, Naeema 8, Jamila 2 and Shahid 14
Exercise 10
1.(62,57) 2. (147) 3. (20, 30) 4. (7, 1) 5. (49) 6. (45, 15) 7. Rs.40500 8. (120) 9. 1710.1 meters 10. (238, 50)
Exercise 11
1. (138, 48) 2. (57) 3. bd: 18.6869 4. Angle D: 53.220 5. 7000 meters 6. (72.71, 23.4) 7. 30.57 cm.
Exercise 12
1. 63.62 sq inch 2. 2213 sq cm 3. 428.869 4. 282.74 cubic feet and 139 buckets 5. 48000 bricks and 125 sq feet.
Exercise 13
1.110.520 2. 81.39 3. 84.51 4. 97.46 5. 92:27, 105:53, 91:38, 57:42, 56:44, -41:52, -38:22, 99:02, 71:29, 13 -5, 0.0,964, 1092.25, 912.77, 11294.9, 10750.98.
Conversion of Sharia Weights